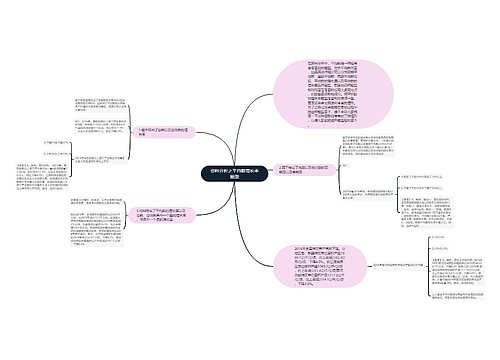
资料分析中的容斥问题，你学会了吗？思维导图

女痞

2023-03-03

浏览量: 3

行测

备考

考试

资料分析中的容斥问题你见过吗？没见过，没关系。它考查的频率不是很高，但不代表不会出现。资料分析中的容斥问题主要以两集合为主，三集合类型还未出现。接下来，一起探究容斥问题在资料分析中出现的几种类型。

树图思维导图提供《资料分析中的容斥问题，你学会了吗？》在线思维导图免费制作，点击“编辑”按钮，可对《资料分析中的容斥问题，你学会了吗？》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：371304ed0784b7c44d059222630cbdd6

思维导图大纲

2019年春节期间有"餐饮消费"的受访居民中，一定有人去：

A.参加教育培训B.去旅游

C.购保健产品D.购数码产品、智能家电

【答案】A

【解析】第一步，本题考查其他计算。

第二步，定位至图形，依据题干2019年春节期间"餐饮消费"受访居民占比为70.2%，"参加教育培训"受访居民占比为33.2%，"去旅游"受访居民占比为27.9%，"购保健产品"受访居民占比为14.9%，"购数码产品、智能家电"受访居民占比为16.0%。

第三步，根据两集合公式，在二集合容斥原理中，总数U为100%，则只需A+B>100%即可满足A中一定有人去B，要想"餐饮消费"受访居民中一定有人去参加另一个消费项目，则使二者占比加和>100%即可。"餐饮消费"受访居民占比70.2%，两个项目占比满足大于100%的只有"参加教育培训"(33.2%)。

因此，选择A选项。

小结：A中一定有B或者A中不一定有B类型解题方法：A+B>100%或者<100%即可。

(2)""至少类型

【例2】某市统计局在针对噪音扰民的一次调查中，当问及是否支持广场舞活动时，12.8%的受访市民表示无所谓或者不知道，12.0%的受访者回答表示反对，其他为支持者。在支持的市民中，当被问及支持的主要原因(多选)时，不同年龄段受访者的回答如下表。

支持广场舞等活动的受访市民选择各主要原因的比例(%)

此次调查中，在支持广场舞等活动的受访青年市民中，同时选择"中老年人的正常锻炼娱乐活动"和"有利于中老年人扩大社交、排解孤独"的至少有：

A.64.7%B.35.3%

C.30.7%D.28.6%

【答案】C

【解析】第一步，本题考查其他计算。

第二步，定位至表格材料"中老年人的正常锻炼娱乐活动"和"有利于中老年人扩大社交、排解孤独"所在行;受访青年中"中老年人的正常锻炼娱乐活动"占比为66%，"有利于中老年人扩大社交、排解孤独"的占比为64.7%。

第三步，问的是"同时选择中老年人的正常锻炼娱乐活动和有利于中老年人扩大社交、排解孤独的至少"的情况，即把选择中老年人的正常锻炼娱乐活动的当作A集合，选择有利于中老年人扩大社交、排解孤独的当作B集合，两者要最少(最少)，即二者尽可能不重合。根据两集合容斥原理：，即，总数U要尽可能的多，最多就是100%，故同时选择"中老年人的正常锻炼娱乐活动"和"有利于中老年人扩大社交、排解孤独"的至少为：66%+64.7%-100%=30.7%。

因此，选择C选项。

小结：""至少类型解题方法：A+B-100%即可。

(3)两集合容斥公式类()

【例3】截至2019年末，全国已有残疾人康复机构9775个，比2018年增长739个。2019年，1043.0万残疾儿童及持证残疾人得到基本康复服务，其中包括0鈥�6岁残疾儿童18.1万人。

如提供视力残疾康复服务的残疾人康复机构中，同时提供听力言语残疾康复服务的机构比不提供该服务的机构多20%，则2019年末全国有多少家残疾人康复机构不提供以上两种康复服务中的任意一种?

A.不到7300家B.7300鈥�7600家之间

C.7600鈥�7900家之间D.超过7900家

【答案】B

【解析】第一步，本题考查其他计算中的二集合容斥原理类。

第二步，很多考生读不懂题干，其实题干中出现的"主体"并不多，就是两个，第一个是视力残疾康复服务的残疾人康复机构，第二个是听力言语残疾康复服务的机构，不妨把第一个当作A集合，第二个当作B集合，题干中说供视力残疾康复服务的残疾人康复机构中，同时提供听力言语残疾康复服务的机构比不提供该服务的机构多20%，"同时提供"说明两集合存在交集()，"不提供"该服务但又在视力残疾康复服务的残疾人康复机构中，说明只提供A不提供B。而题目所求为残疾人康复机构不提供以上两种康复服务中的任意一种，即求的就AB补集部分()，如果还不理解的话，最好结合画图法(如下图所示)。

当题干梳理清楚以后，定位文字材料可知，"截至2019年末，全国已有残疾人康复机构9775个"，定位图形可知，"2019年末，提供视力残疾康复服务的康复机构的数量为1430个、提供听力言语残疾康复服务的康复机构的数量为1669个"。设只提供视力残疾康复服务的残疾人康复机构为，两者都提供的即为，即，。两者都提供的。根据两集合型公式：可得：康复机构数(U)=视力残疾康复服务的康复机构(A)+听力言语残疾康复服务的康复机构(B)-同时提供视力和听力言语残疾的康复机构()+两种康复机构都不提供()，代入数据可得：，即。

因此，选择B选项。

小结：正常用两集合公式解题即可。

思维导图：

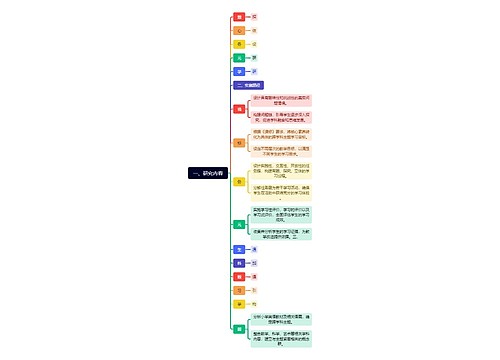
一、研究内容思维导图