行测数量关系技巧之比例方法思维导图
深拥意中人
2023-03-03
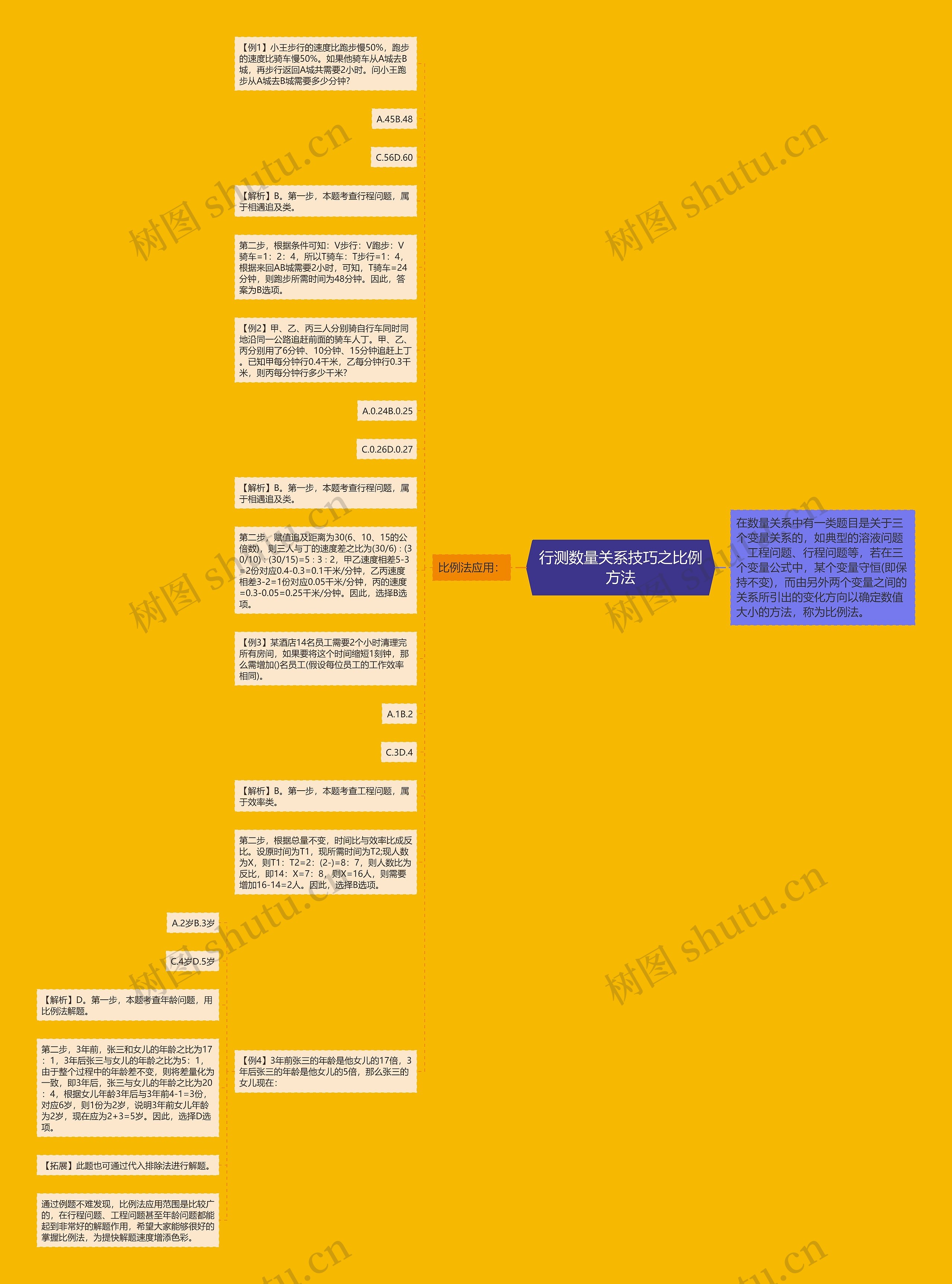
在数量关系中有一类题目是关于三个变量关系的，如典型的溶液问题、工程问题、行程问题等，若在三个变量公式中，某个变量守恒(即保持不变)，而由另外两个变量之间的关系所引出的变化方向以确定数值大小的方法，称为比例法。
树图思维导图提供《行测数量关系技巧之比例方法》在线思维导图免费制作，点击“编辑”按钮，可对《行测数量关系技巧之比例方法》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：d477ecd4c7f3b749105c7f6b18ab10b3
思维导图大纲
相关思维导图模版
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作，点击“编辑”按钮，可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：10b9a8a2dd2fb4593f8130ef16c320fc
抓住重点思维导图
~漫埗陽茪~树图思维导图提供《抓住重点》在线思维导图免费制作，点击“编辑”按钮，可对《抓住重点》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：4c49e4799ddf94a339c56e46eb96a826
