经验分享：行程问题中的相遇追及类问题思维导图

雨过之后

2023-03-03

浏览量: 4

2023国考

数量关系

行测备考

行程问题无论在公考还是事业单位考试中都是常客，大家对于行程问题的学习可谓又爱又恨，一方面基本行程问题出现后我们发现难度并不高，另一方面相遇追及问题出现的时候却容易迷惑。

树图思维导图提供《经验分享：行程问题中的相遇追及类问题》在线思维导图免费制作，点击“编辑”按钮，可对《经验分享：行程问题中的相遇追及类问题》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：348cf039ec9e9675a4289d29e962ab04

思维导图大纲

我们先来看一下相遇追及问题相关内容：

通过图我们发现，相遇追及可以划分为直线和环形两大类。但是通过观察公式发现，相遇的公式都是速度做"相加"运算，追及的公式都是速度做"相减"运算，可谓异曲同工。在记忆的时候不用刻意的分成两类，我们只需要理解相遇是两个物体相向而行，那么最终共同的运动必然是两个速度合成的结果;追及是两个物体同向而行，为了达到追上的目的，必然是用一方的速度去减去另一方的速度才可以实现。在具体应用的过程中，一定要看清楚题目中的运动形式，从而选取正确的解题公式。

我们通过一个题目来看一下相遇追及公式的应用。

【例1】某宣讲团甲宣传员骑摩托车从红星村出发以20公里/小时的速度去相距60公里的八一村，1小时后由于路面湿滑，速度减少一半，在甲出发1小时后，乙宣传员以50公里/小时的速度开车从红星村出发追甲，当乙追上甲时，他们与八一村的距离为多少?

A.25公里B.40公里

C.35公里D.30公里

我们一起来看一下这个题目。从问法上来说，此题属于行程问题中的追及类问题，我们分析一下，追及问题的公式是：S=(V1-V2)脳T，这里由于路程S是甲宣传员骑摩托车拉开的距离，即S=20脳1=20公里，后面乙宣传员追及的过程中，甲的速度已经减少了一半，变成了10公里/小时，因此追及的过程为：20=(50-10)脳T，解得T=0.5小时。接下来求解他们相距终点八一村的距离可以列得：60-50脳0.5=35公里。因此选择C选项。

最近几年相遇追及问题也是频频登上黑龙江公考的试卷，我们通过一道黑龙江的真题来一起巩固一下相遇追及的知识点。

【例2】(2021年1228黑龙江公务员考试-63)某圆形跑道长为400米，甲从跑道上A点以6米/秒的速度顺时针跑步前行。乙在A点对应直径的另一端B点同时以5米/秒的速度逆时针跑步前行，问在14分钟内，他们共相遇了多少次?()

A.22B.23

C.24D.25

还是先看题目特征，通过问题可知此题考察的是行程问题中的相遇问题。首先，相遇公式为：S=(V1+V2)脳T。由题干可知，在第一次相遇时，两人相遇总路程为200米，用时秒，大家一定要注意，这个时候他们在同一点位置，之后的每次相遇，路程总和均为跑道一圈的长度400米，所以每次相遇用时秒，假设第一次相遇之后又相遇了a次，总用时+a脳=14脳60，解得a=22.6，取整可得a=22，所以共相遇22+1=23次。因此，选择B选项。

通过今天的学习，大家一定会对行程问题特别是相遇追及类问题有一个全局的认识，在今后的学习中一定要多加练习，在公考中攻坚克难。

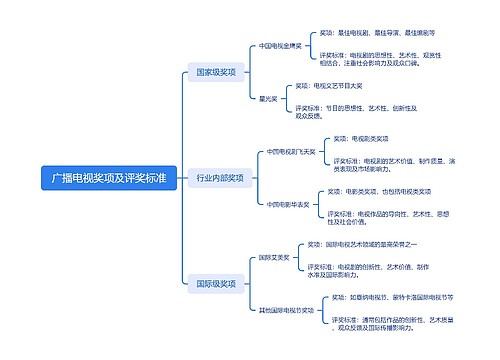
广播电视奖项及评奖标准思维导图