熵与信息思维导图
女痞
2023-02-21
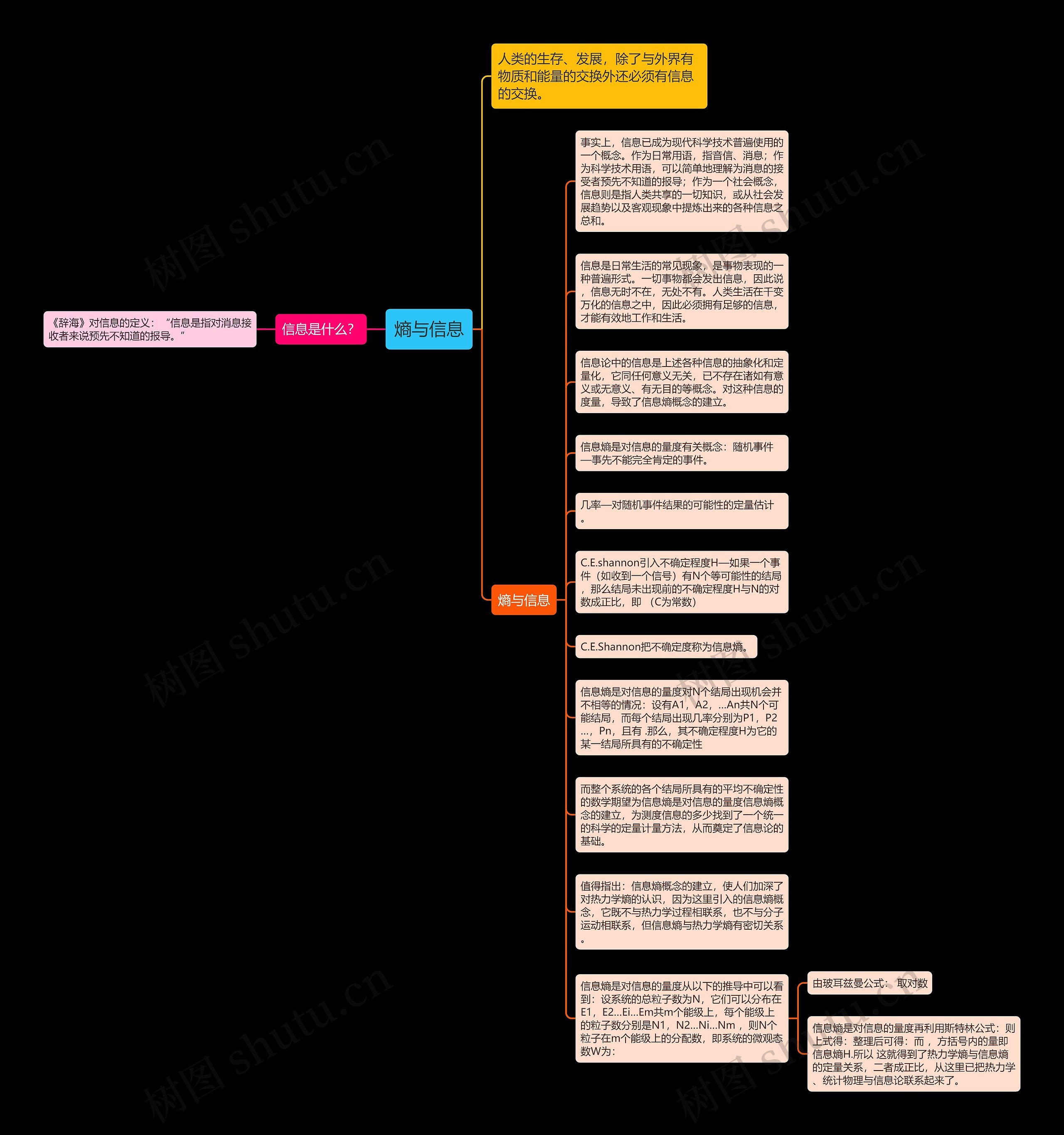
人类的生存、发展,除了与外界有物质和能量的交换外还必须有信息的交换。 信息是什么? 《辞海》对信息的定义:“信息是指对消息接收者来说预先不知道的报导。” 熵与信息 事实上,信息已成为现代科学技术普遍使用的一个概念。
树图思维导图提供《熵与信息》在线思维导图免费制作,点击“编辑”按钮,可对《熵与信息》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:0834da6e0db709e0e1c6cb3bf74dc2ef

人类的生存、发展,除了与外界有物质和能量的交换外还必须有信息的交换。 信息是什么? 《辞海》对信息的定义:“信息是指对消息接收者来说预先不知道的报导。” 熵与信息 事实上,信息已成为现代科学技术普遍使用的一个概念。
树图思维导图提供《熵与信息》在线思维导图免费制作,点击“编辑”按钮,可对《熵与信息》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:0834da6e0db709e0e1c6cb3bf74dc2ef