竖直上抛运动的定义及公式思维导图
心不动则不痛
2023-01-13
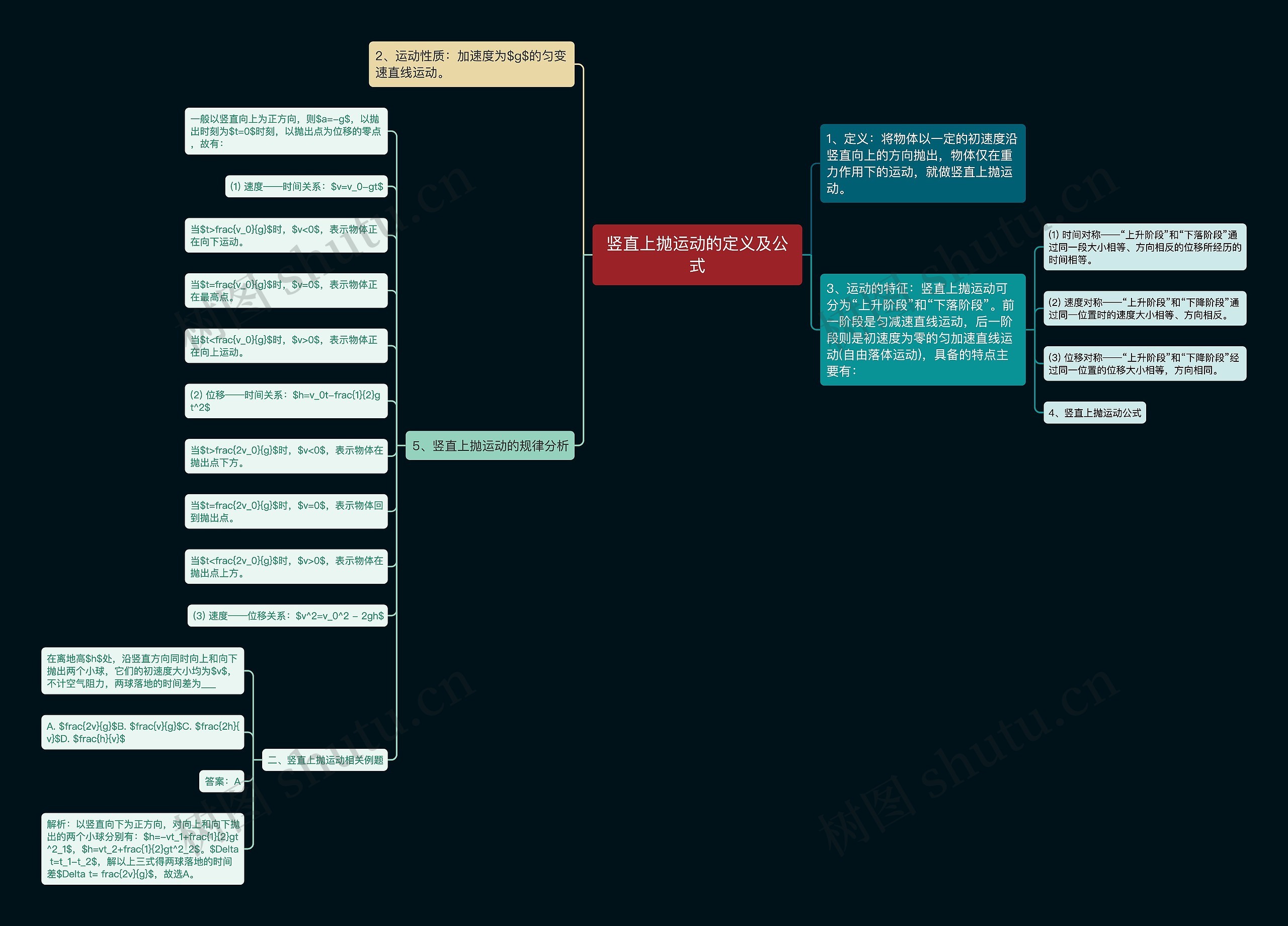
一、竖直上抛运动的定义及公式
树图思维导图提供《竖直上抛运动的定义及公式》在线思维导图免费制作,点击“编辑”按钮,可对《竖直上抛运动的定义及公式》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:d5577584328fae12fef5b57978e86b07

一、竖直上抛运动的定义及公式
树图思维导图提供《竖直上抛运动的定义及公式》在线思维导图免费制作,点击“编辑”按钮,可对《竖直上抛运动的定义及公式》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:d5577584328fae12fef5b57978e86b07