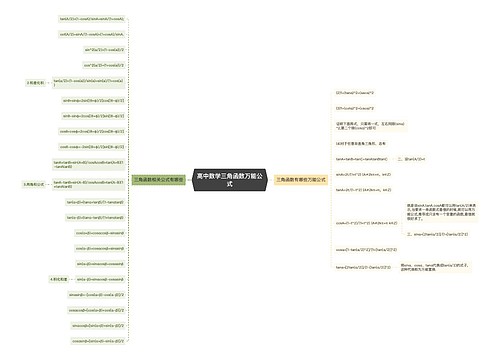
三角函数万能公式有哪些思维导图
心不动则不痛
2023-01-12
有很多的同学是非常的想知道，三角函数万能公式有哪些，小编整理了相关信息，希望会对大家有所帮助！
树图思维导图提供《三角函数万能公式有哪些》在线思维导图免费制作，点击“编辑”按钮，可对《三角函数万能公式有哪些》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：e3b3704f98f3680b254dc99aa41fecef
思维导图大纲
相关思维导图模版
乌审旗国有投资集团有限公司思维导图
U682198976树图思维导图提供《乌审旗国有投资集团有限公司》在线思维导图免费制作，点击“编辑”按钮，可对《乌审旗国有投资集团有限公司》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：5a28142386bd70b085d0dfa0b38ffb1d
说文解字戏美国总统大选思维导图
fishfol树图思维导图提供《说文解字戏美国总统大选》在线思维导图免费制作，点击“编辑”按钮，可对《说文解字戏美国总统大选》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：062e27e31bfd81ad6f3ed78f2a4c7de2
