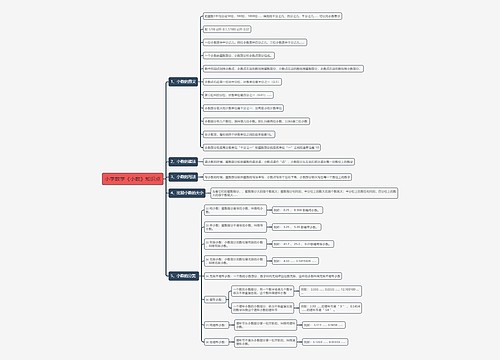
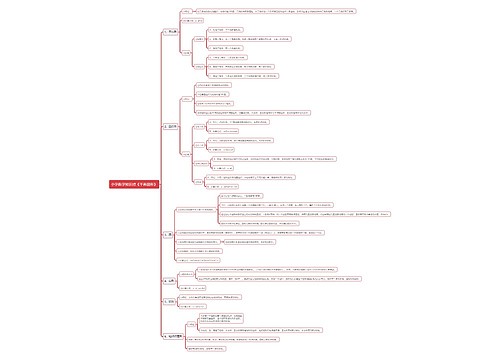
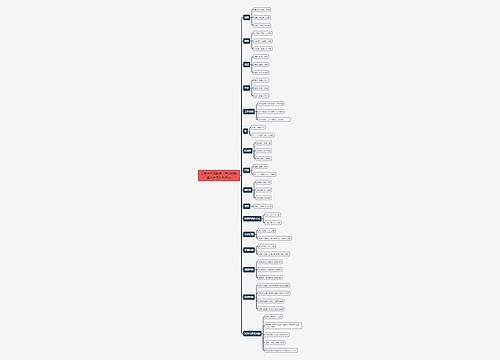
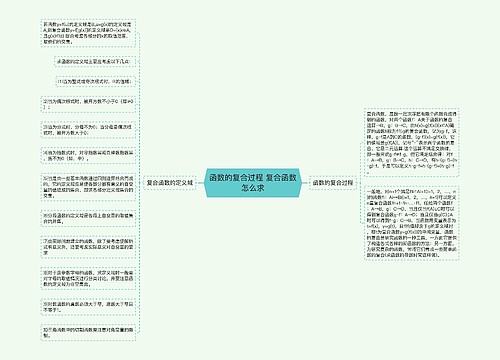
高中数学第二次求导的意义是什么 二阶导数有哪些意义思维导图

高中数学第二次求导的意义是表示函数图象在某点的切线的斜率变化快慢，也代表着函数值的变化率的变化快慢，类似于位移二次求导即加速度。常见的二阶导数的几何意义包含切线斜率变化的速度和函数的凹凸性，即函数值的增加和减少的速度和函数的图形形状，如果二阶导数大于零，则函数在该区间上为凹的，若小于零，则函数为凸的。在函数可导的定义上，函数一点可导需要左右导数存在且相等且该点连续，否则不可导，可导的函数一定连续，但连续的函数不一定可导，不连续的函数一定不可导。