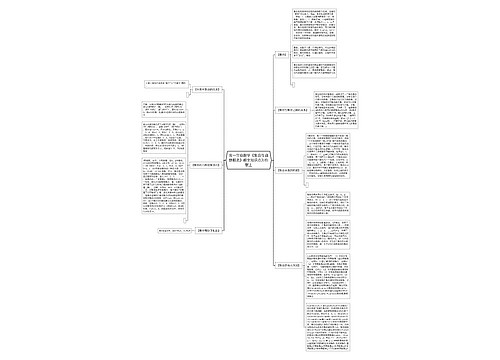
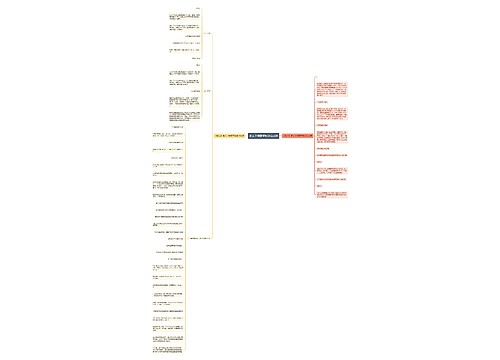
高三数学基础知识学习方法思维导图
叹黄昏
2022-12-21

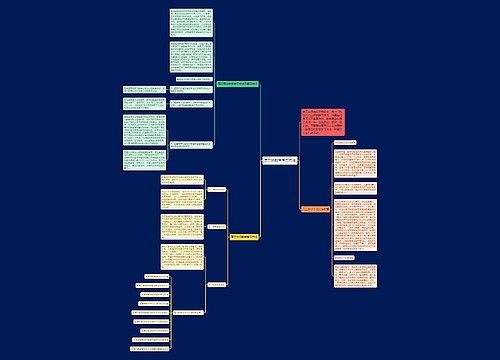
高三数学基础知识学习方法思维导图首先要注意题目的难度适宜,循序渐进,不可好高骛远,在练习时要注重细节而不是数量,贵在精,第三要重视改错,记录错误原因及教训,第四要重视总结,掌握基本题及思想原理。同时要重视课本中的定义、定理、公式,深刻理解其内涵与外延和运用条件和范围,加深对典型命题所体现的思想与方法的理解和掌握,只有以上方法的综合运用,才能提高自己的数学水平,为高考取得好成绩打下坚实的基础。
思维导图大纲
相关思维导图模版
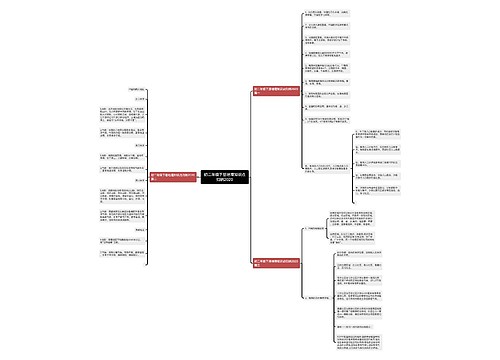
高三数学不及格的学习方法建议思维导图
 何苦孤独
何苦孤独树图思维导图提供《高三数学不及格的学习方法建议》在线思维导图免费制作,点击“编辑”按钮,可对《高三数学不及格的学习方法建议》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:ec5b668deb971d68708b585748c48af1
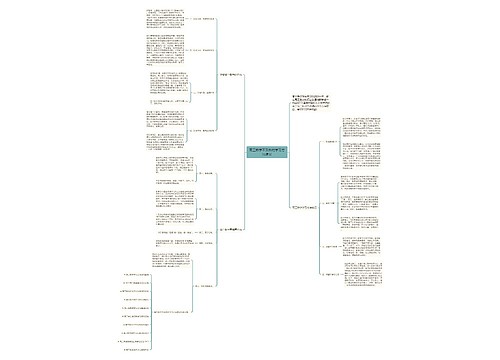
高三数学零基础学习方法思维导图
 余生愿你常欢笑
余生愿你常欢笑树图思维导图提供《高三数学零基础学习方法》在线思维导图免费制作,点击“编辑”按钮,可对《高三数学零基础学习方法》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6a6f2bc597c801bfaeb23a8f5b50c33c