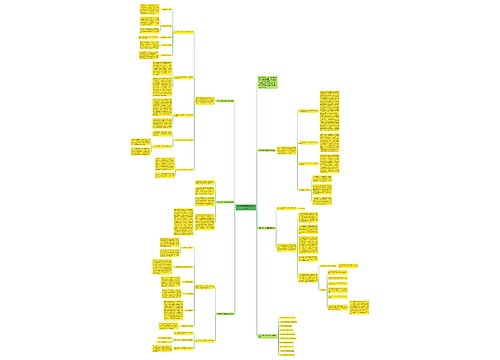
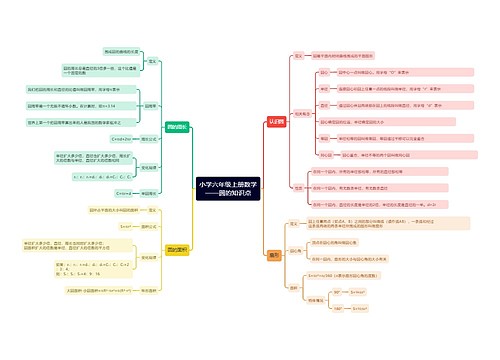
1、一个物体、一个计量单位或由许多物体组成的一个整体,都可以用自然数1来表示,通常我们把它叫做单位“1”。把单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数。表示其中一份的数,叫做分数单位。一个分数的分母是几,它的分数单位就是几分之一。
3、举例说明一个分数的意义:3/7表示把单位“1”平均分成7份,表示这样的3份.还表示把3平均分成7份,表示这样的1份。3/7吨表示把1吨平均分成7份,表示这样的3份.还表示把3吨平均分成7份,表示这样的1份。
5、分子比分母小的分数叫做真分数;分子比分母大或者分子和分母相等的分数叫做假分数。
6、真分数小于1。假分数大于或等于1。真分数总是小于假分数。
7、男生人数是女生人数的3/4,则女生人数是男生人数的4/3。
8、分数与除法的关系:被除数相当于分数的分子,除数相当于分数的分母。被除数÷除数= 除数被除数如果用a表示被除数,b表示除数,可以写成a÷b=bab≠0
9、能化成整数的假分数,它们的分子都是分母的倍数。反过来,分子是分母倍数的假分数,都能化成整数。用分子除以分母
10、分子不是分母倍数的假分数,可以写成整数和真分数合成的数,通常叫做带分数。带分数是假分数的另一种形式。例如,4/3就可以看作是3/3就是1和1/3合成的数,读作一又三分之一。带分数都大于真分数,同时也都大于1。
11、把分数化成小数的方法:用分数的分子除以分母。
12、把小数化成分数的方法:如果是一位小数就写成十分之几,是两位小数就写成百分之几,是三位小数就写成千分之几,……
13、把假分数转化成整数或带分数的方法:分子除以分母,如果分子是分母的倍数,可以化成整数;如果分子不是分母的倍数,可以化成带分数,除得的商作为带分数的整数部分,余数作为分数部分的分子,分母不变。 14、把带分数化成假分数的方法:把整数乘分母加分子作为假分数的分子,分母不变。
15、把不是0的整数化成假分数的方法:用整数与分母相乘的积作分子。
16、大于73而小于75的分数有无数个;分数单位是71只有74一个。
17、分数大小比较的应用题:工作效率大的快,工作时间小的快。
18、求一个数是占另一个数的几分之几,用除法列算式计算。
一、填空
1.把一张长方形的纸对折后再对折,这张纸平均分成了 份,每份是它的 ,写作: 。
2.把一个蛋糕平均分成5块,其中的3块是 分之 , 写作: ,它的分子是 ,分母是 。
一、填空
1.把一张长方形的纸对折后再对折,这张纸平均分成了 4份,每份是它的 四分之一 ,写作:1/4 。
2.把一个蛋糕平均分成5块,其中的3块是 5分之 3 , 写作: 3/5,它的分子是3 ,分母是5 。
二、判断对错
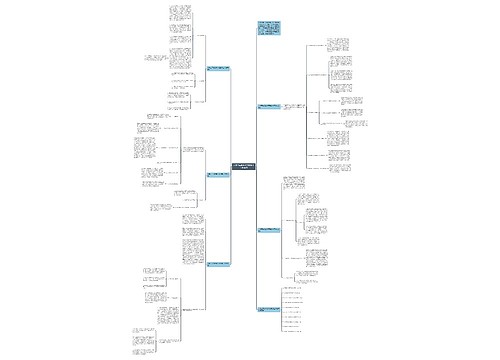
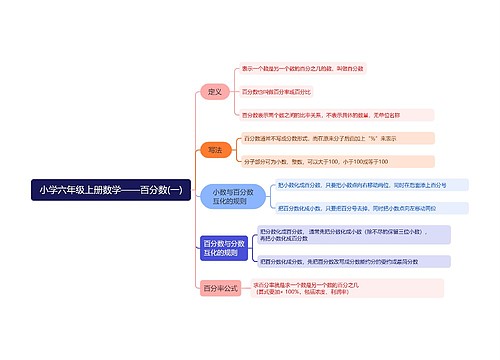
1、面积的定义 物体表面或平面图形的大小 叫做它们的面积。
2、面积的单位:
① . 边长为 1厘米的正方形 , 面积是 1平方厘米 , 也可以写作 1厘米 2或 cm 2 。 如橡皮、邮票、硬币等。
② . 边长为 1分米的正方形 , 面积是 1平方分米 , 也可以写作 1分米 2或 dm 2 。 如课本面、书桌面等。
③ . 边长为 1米的正方形 , 面积是 1平方米 , 也可以写作 1米 2或 m2 。 如黑板面、教室地面、花坛、操场等。
3、常用的面积单位:
平方米 m 2 、平方分米 dm 2 、平方厘米 cm 2 。
1m 2=100 dm2=10000 cm2、 1dm 2=100 cm2
4、常用的长度单位:米、分米、厘米。
8000 cm2= dm 2 30000 cm2= m2
2m 230 dm2= dm2 4dm 260 cm2= cm2
正方形周长 =边长×4; 边长 =周长÷4 正方形面积 =边长×边长 8
正方形,边长扩大 n 倍,周长扩大 n 倍,面积扩大 n ×n 倍。
正方形,边长增加 n ,周长增加 n ×4,面积增加 n ×n 。
2正方形的边长是8分米,它的面积是 64平方分米。
1、一个平行四边形的底是12厘米,面积是156平方厘米,高是 厘米。
2、一块平行四边形钢板,底是1.5米,高是1.2米,如果每平方米钢板重23.5千克,这块钢板重 千克。
3、等底等高的平行四边形面积都 。一个平行四边形的周长为46厘米,一边的长为14厘米,另外三边的长分是 、 、 。
1、一个平行四边形的底是12厘米,面积是156平方厘米,高是13 厘米。
2、一块平行四边形钢板,底是1.5米,高是1.2米,如果每平方米钢板重23.5千克,这块钢板重42.3 千克。
3、等底等高的平行四边形面积都 相等 。一个平行四边形的周长为46厘米,一边的长为14厘米,另外三边的长分是 14、 9、9 。

 自我孤立
自我孤立
 我没你想的那样坚强
我没你想的那样坚强