小学数学经典教案模板范文(7篇)思维导图
我有一颗少女心耶
2023-05-09

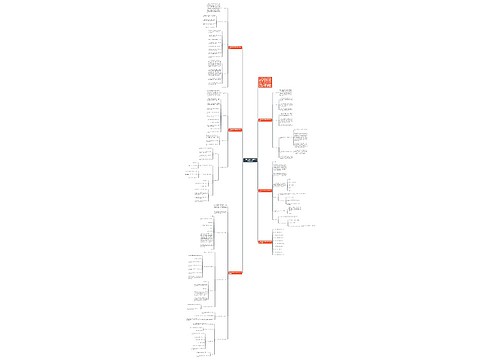
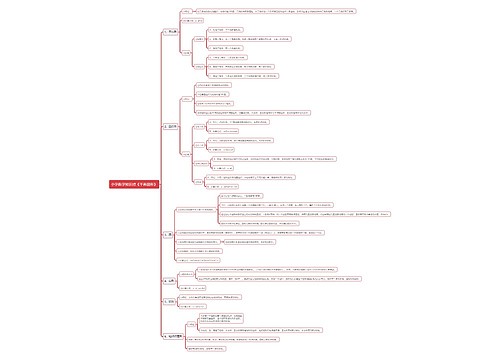
模板展示了小学数学经典教案模板范文的知识点,首先是教学内容、教学目标和教学重点、难点、关键,接着介绍了教学方法,包含复习旧知识、传授新知识、巩固新知识的顺序启发式教学方法,还提供了一些教学过程中常用的提示语。板书设计、教学小结、教学反思,该文还给出了一些学习例题,供学生在课下进行练习。
总结起来,模板展示了小学数学经典教案模板范文的相关内容,包含教学目标、教学重点、教学方法、板书设计,通过教学过程中的复习、讨论和练习,帮助学生掌握相关知识,并思维能力。
思维导图大纲
相关思维导图模版
小学一年级数学上册九加几教案范文思维导图
 空城旧人
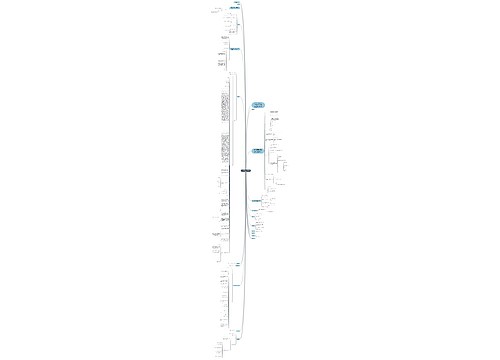
空城旧人树图思维导图提供《小学一年级数学上册九加几教案范文》在线思维导图免费制作,点击“编辑”按钮,可对《小学一年级数学上册九加几教案范文》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:c8edceb8aa41296428a8f4ec8674b4b1

一年级上册新人教数学优秀教案范文思维导图
 凉笙微凉
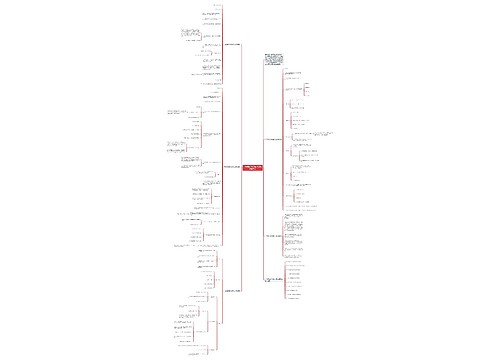
凉笙微凉树图思维导图提供《一年级上册新人教数学优秀教案范文》在线思维导图免费制作,点击“编辑”按钮,可对《一年级上册新人教数学优秀教案范文》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:fbb483db0e619626d11843edf1b05475