等比数列思维导图
您L
2023-05-08
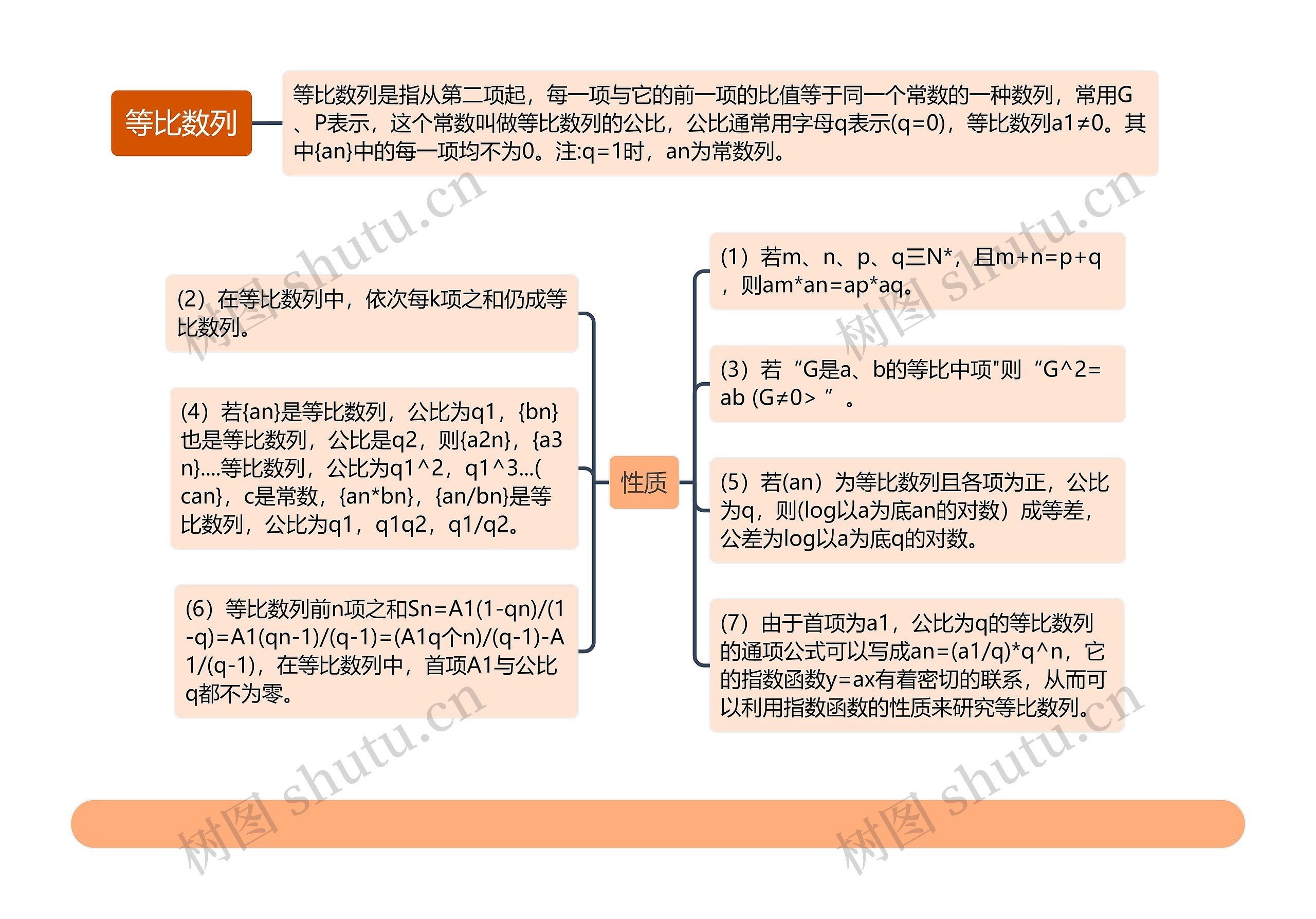
这篇思维导图介绍了等比数列
树图思维导图提供《等比数列》在线思维导图免费制作,点击“编辑”按钮,可对《等比数列》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:a8da5bfa9cbab394f79912f9c27c091e

这篇思维导图介绍了等比数列
树图思维导图提供《等比数列》在线思维导图免费制作,点击“编辑”按钮,可对《等比数列》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:a8da5bfa9cbab394f79912f9c27c091e