高二数学：几何的三大问题思维导图

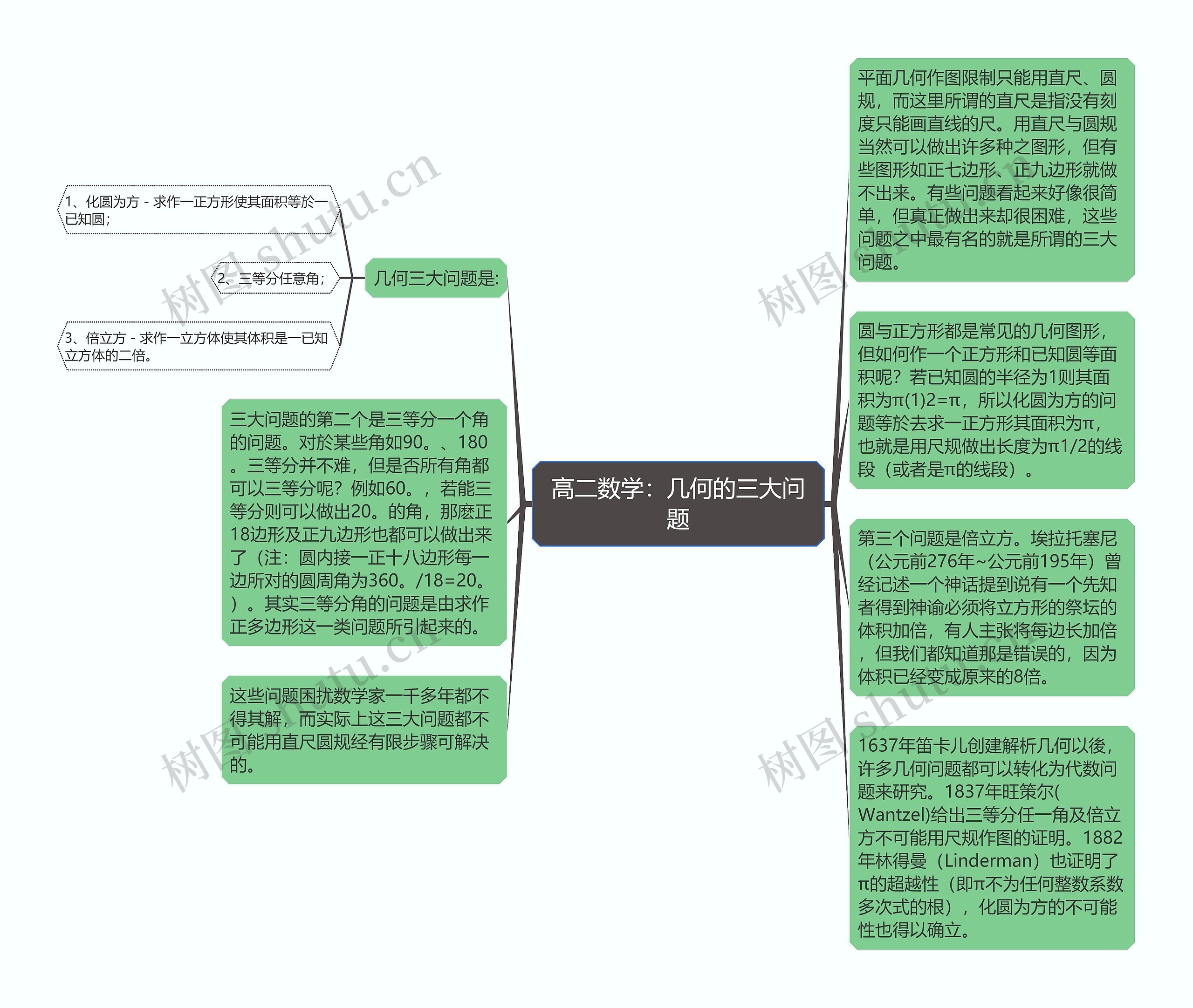
高二数学：几何的三大问题思维导图包含：-化圆为方：求作一个正方形，使其面积等于一个已知圆。

-三等分任意角：如何将任意角分成三份。

-倍立方/：如何构造一个立方体，使其体积是一个已知立方体的两倍。

在平面几何作图中，只能使用直尺和圆规。虽然直尺和圆规能做出许多图形，但有些特殊图形如正七边形和正九边形无法用直尺和圆规作出，其中最著名的三大问题是三个难题。

第一个问题是化圆为方。要求作一个正方形，使其面积等于一个已知圆的面积。圆与正方形是常见的几何图形，但如何找到一个正方形和已知圆面积呢？该问题实际上是要找到一个长度为π的线段，而π是一个无理数，无法用有限的步骤用尺规作出。

第二个问题是三等分任意角。尽管对于某些角如90度、180度三等分并不难，但对于所有角来说是否都可以三等分呢？该问题实际上与求作正多边形有关。

第三个问题是倍立方。早在公元前的时候就有一位先知者得到了神谕，要将一个立方体的体积加倍，有人主张将每条边的长度加倍，但这是错误的，实际上，这个问题无法用直尺和圆规经有限步骤解决。

这些问题困扰了数学家数千年。但自从1637年笛卡尔创建了解析几何以后，许多几何问题都可以转化为代数问题来研究，1837年，旺策尔证明了三等分任一角和倍立方问题无法用尺规作图，1882年，林得曼证明了π的超越性和化圆为方的不可能性，这三个问题无法用直尺和圆规解决。