高二数学备考：几何的三大问题思维导图

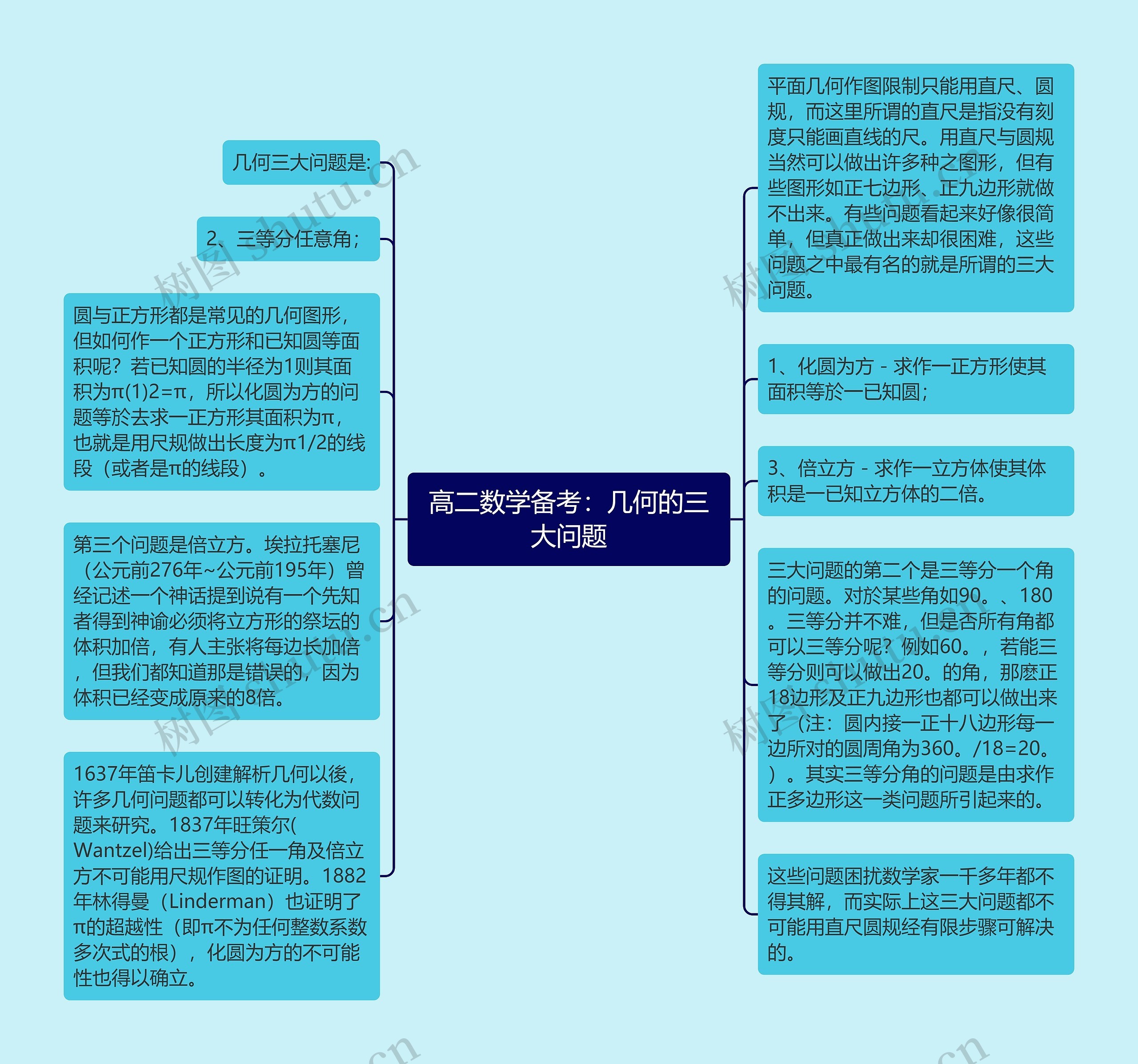
高二数学备考：几何的三大问题思维导图模板大纲是学习平面几何作图的限制和所用工具，如直尺和圆规，尽管使用这些工具可以画出多种图形，但某些图形如正七边形和正九边形却无法实现，在几何学中，存在一些问题看似简单，但实际上却很理解困难，其中最著名的就是三大问题。这三大问题包含将圆化为方，即找到一个正方形面积与给定圆相等，将任意角三等分，和找到一个立方体体积是给定立方体的两倍。圆与正方形都是常见的几何图形，但如何找到一个与给定圆面积的正方形呢？若已知圆的半径为1，则其面积为π，因此化圆为方的问题等同于找到一个边长为π的线段。在三等分角的问题中，对于一些角如90度或180度，三等分并不理解困难，但是否所有角都可以三等分呢？如果可以将60度三等分，则可以构造出20度的角，可以绘制正18边形和正九边形。实际上，三等分角的问题与构造正多边形的问题有关，第三个问题是倍立方，根据一个神话故事，有一个先知被迫将立方体的体积加倍，但将每条边加倍是错误的，因为体积将增加到原来的8倍。这些问题困扰了数学家们长达一千多年，实际上这三个问题都无法用有限步骤的直尺和圆规解决，自1637年笛卡儿创立解析几何以来，许多几何问题都可以转化为代数问题进行研究，1837年，旺策尔证明了无法用尺规三等分任意角和倍立方，1882年，林得曼证明了π是超越数（即π不是任何整系数多项式的根），确立了化圆为方不可能的性质。