高一数学知识点:直线和平面的位置关系思维导图
谁相伴
2023-04-20

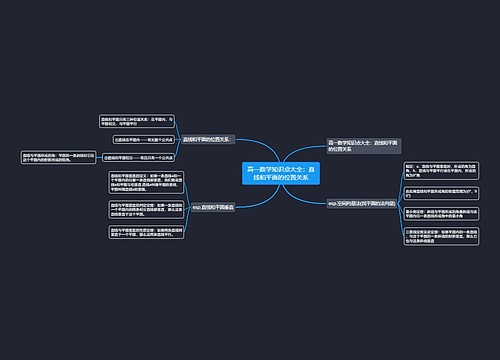
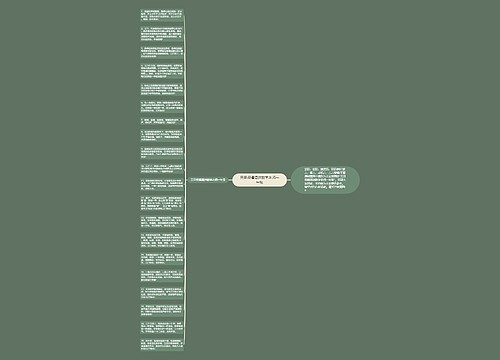
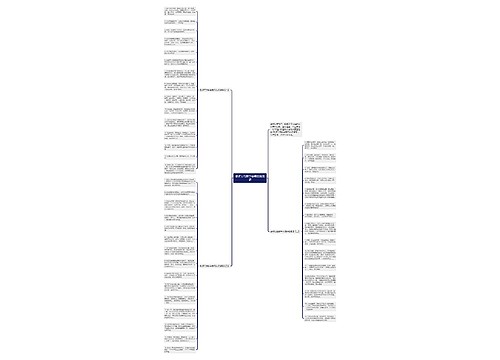
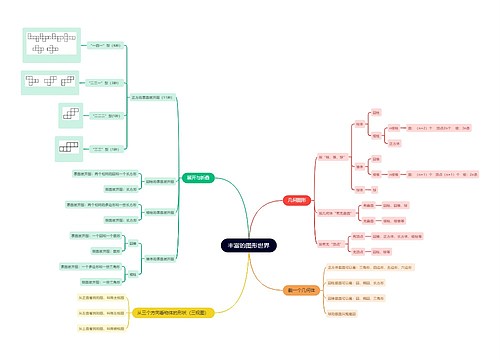
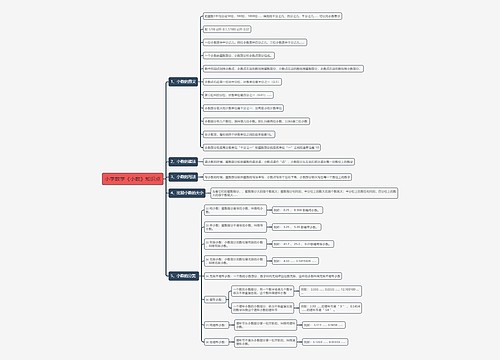
高一数学知识点:直线和平面的位置关系思维导图,直线和平面的位置关系一共有三种:在平面内、与平面相交、与平面平行。如果直线平面内,他会有无数个公共点,如果直线和平面相交,他只有一个公共点,直线与平面所成的角可以通过使用空间向量法来确定平面的法向量,规定了两种情况:直线与平面垂直时所成的角是直角,而直线与平面平行或在平面内时所成的角为0°角。直线和平面所成角的取值范围是0°到90°,根据最小角定理,斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角。三垂线定理逆定理告诉我们:如果一条直线与平面的斜线垂直,那么他也与斜线垂直,直线和平面垂直的定义,如果一条直线与平面内的所有直线都垂直,就说直线和平面互相垂直,直线称为平面的垂线,平面则称为直线的垂面。直线和平面垂直的判定定理告诉我们:如果一条直线和平面内的两条相交直线都垂直,那么本直线就垂直于平面。直线和平面垂直的性质定理,如果两条直线都垂直于一个平面,那么这两条直线是平行的,如果一条直线和一个平面没有公共点,那么我们称本直线和平面平行。直线和平面平行的判定定理,如果平面外的一条直线和平面内的一条直线平行,那么本直线和平面平行,如果一条直线和一个平面平行,而通过本直线的平面与该平面相交,那么本直线和交线是平行的。
思维导图大纲
相关思维导图模版
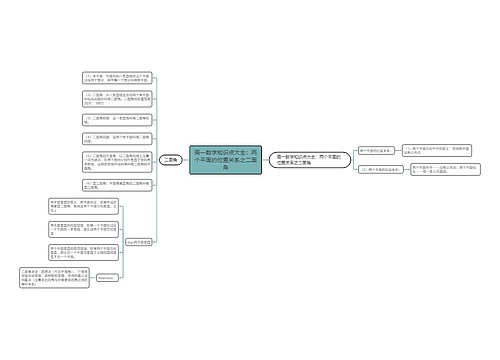
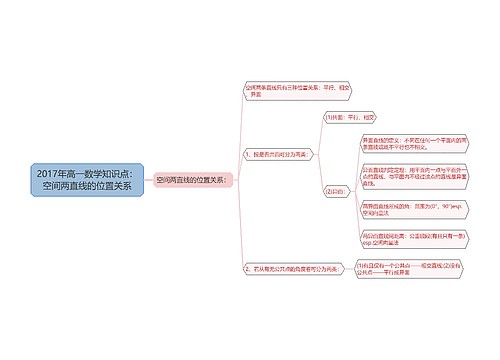
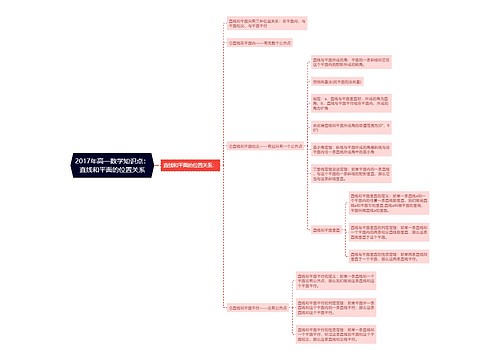
2017年高一数学知识点:直线和平面的位置关系思维导图
 丸子家的猫
丸子家的猫树图思维导图提供《2017年高一数学知识点:直线和平面的位置关系》在线思维导图免费制作,点击“编辑”按钮,可对《2017年高一数学知识点:直线和平面的位置关系》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:45470003049b003a32132f8d8d371656
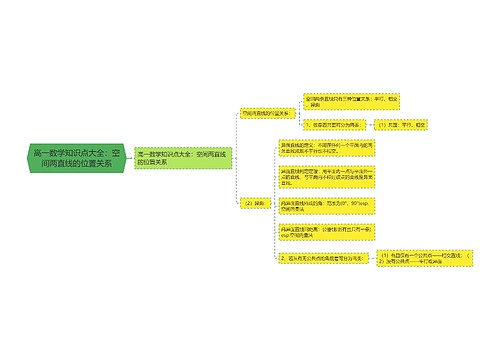
高一数学《空间点、直线、平面的位置关系》知识点总结思维导图
 女痞
女痞树图思维导图提供《高一数学《空间点、直线、平面的位置关系》知识点总结》在线思维导图免费制作,点击“编辑”按钮,可对《高一数学《空间点、直线、平面的位置关系》知识点总结》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:97d9886ee4d9c6c42dd5bddc6cbe142f