高一数学知识点大全：两个平面的位置关系之二面角思维导图

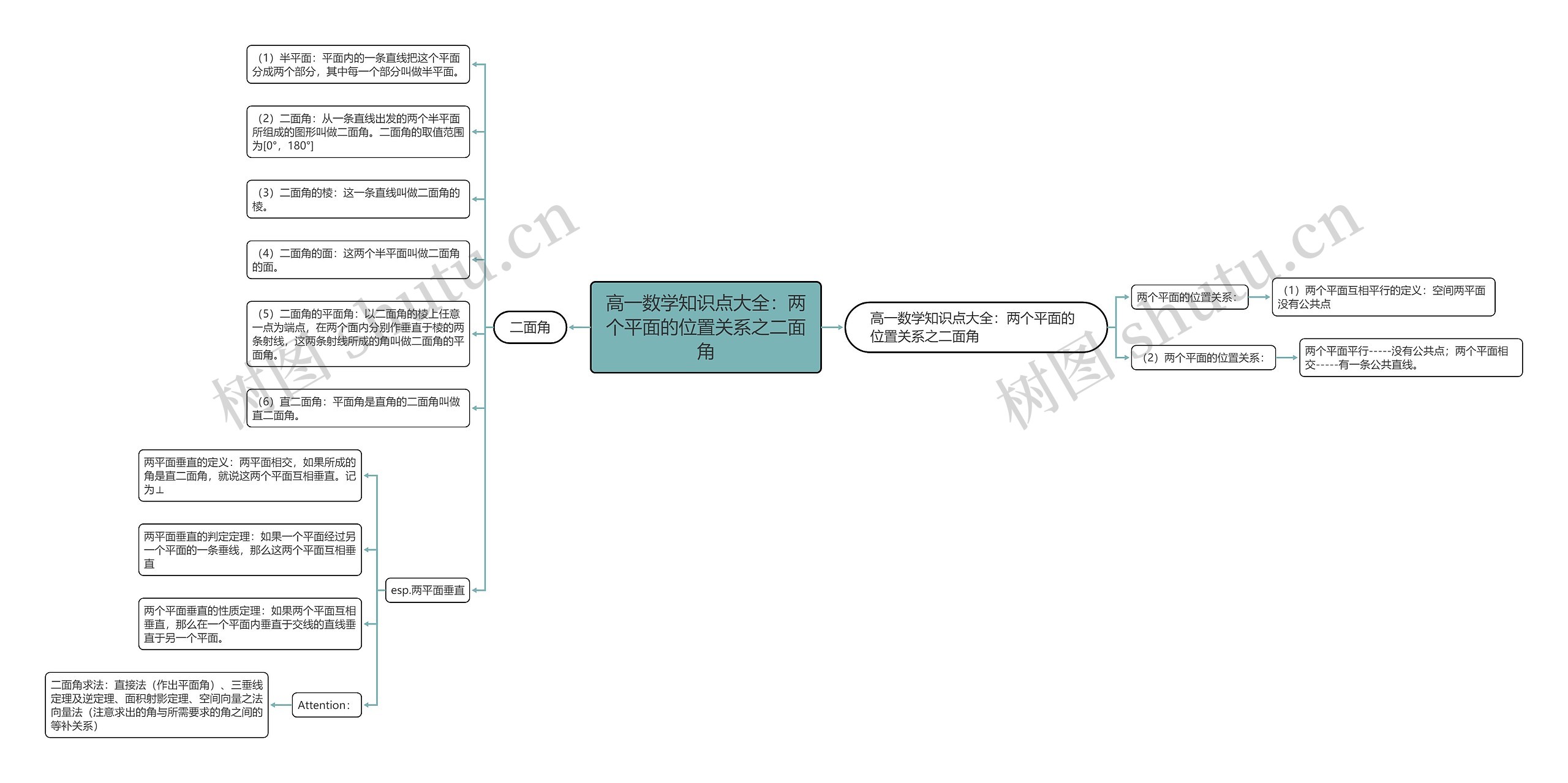
高一数学知识点大全：两个平面的位置关系之二面角思维导图，/在高一数学中，学习了关于两个平面的位置关系和二面角的概念。两个平面互相平行的定义是指这两个平面没有公共点，而两个平面的位置关系有两种情况：平行和相交，当两个平面平行时，他没有公共点，而当两个平面相交时，他有一条公共直线。

在二面角的概念中，我们首先介绍了半平面的概念，即平面内的一条直线将该平面分成两部分，称之为半平面。而二面角则由从一条直线出发的两个半平面组成，二面角的取值范围在0°到180°之间，二面角的棱是指二面角的那条直线，而二面角的面指的是二面角的两个半平面。

我们还介绍了二面角的平面角，即以二面角的棱上的任意一点为端点，在两个面内作垂直于棱的两条射线，这两条射线所成的角就是二面角的平面角。特别地，当平面角是直角时，称之为直二面角。

当讨论两个平面垂直的情况时，两个平面相交，且所成的角是直二面角，称这两个平面互相垂直，记作⊥。两个平面垂直的判定定理，当一个平面经过另一个平面的一条垂线时，这两个平面互相垂直，两个平面垂直的性质定理，如果两个平面互相垂直，那么在一个平面内垂直于交线的直线也垂直于另一个平面。

在求解二面角时，可以使用直接法（作出平面角）、三垂线定理及逆定理、面积射影定理、空间向量之法向量法。要注意所求的角与已知角之间的等补关系。

通过以上知识点的学习，可以更好的理解和解决与两个平面的位置关系和二面角相关的问题。