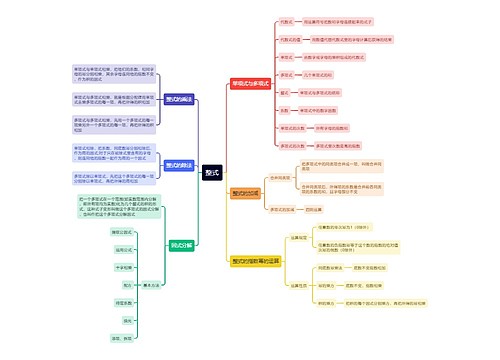
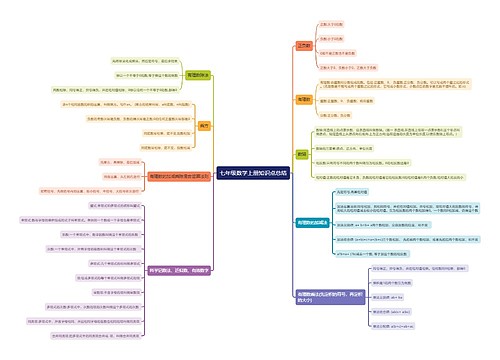
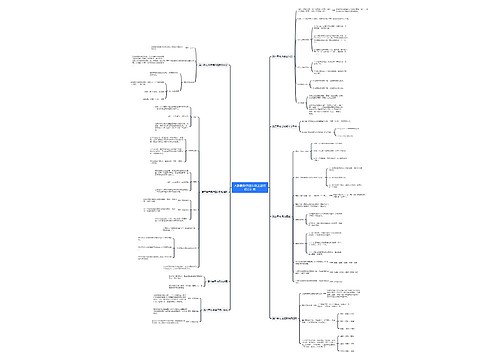
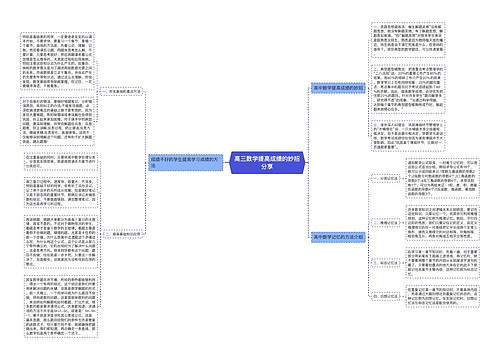
2017年高一数学知识点：立体几何思维导图

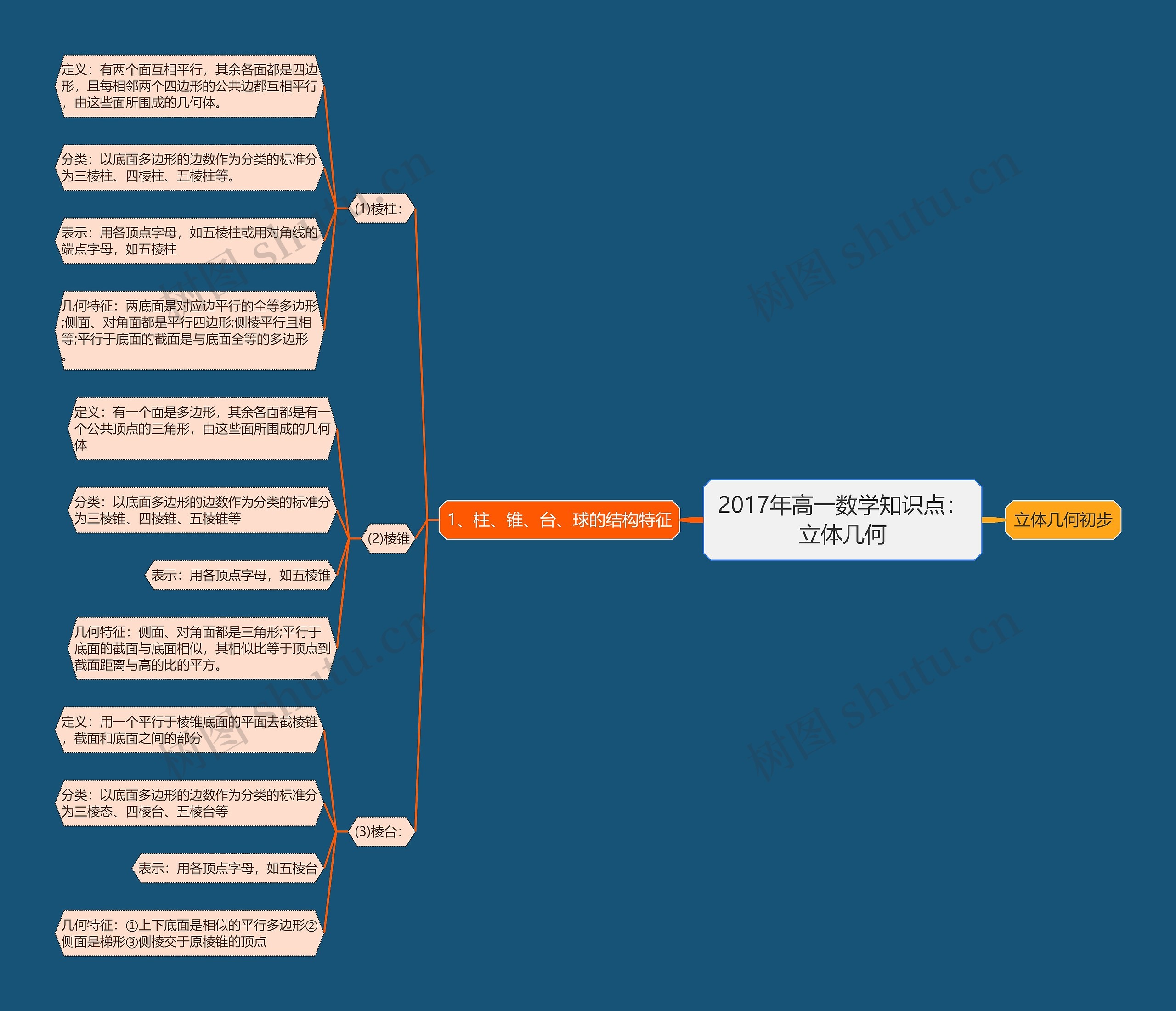
2017年高一数学知识点：立体几何思维导图模板大纲，在立体几何初步的学习中，需要了解柱、锥、台、球的结构特征，对于柱来说，他有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行。柱可以根据底面多边形的边数来分类，比如三棱柱、四棱柱和五棱柱，可以用各顶点的字母来表示柱体，例如五棱柱或用对角线的端点字母来表示，比如五棱柱，柱的几何特征是两个底面对应边平行且全。侧面和对角面都是平行四边形，侧棱平行且相等，而且平行于底面的截面与底面是全等的多边形。对于锥来说，他有一个面是多边形，其余各面都是有一个公共顶点的三角形，锥也可以根据底面多边形的边数来分类，比如三棱锥、四棱锥和五棱锥，可以用各顶点的字母来表示锥体，例如五棱锥。锥的几何特征是侧面和对角面都是三角形，而且平行于底面的截面与底面相似，其相似比于顶点到截面距离与高的比的平方，最后是台，他是用一个平行于锥底面的平面去截锥，截面和底面之间的部分。台也可以根据底面多边形的边数来分类，比如三棱台、四棱台和五棱台，可以用各顶点的字母来表示台体，例如五棱台，台的几何特征是上下底面是相似的平行多边形，侧面是梯形，而且侧棱交于原锥的顶点。