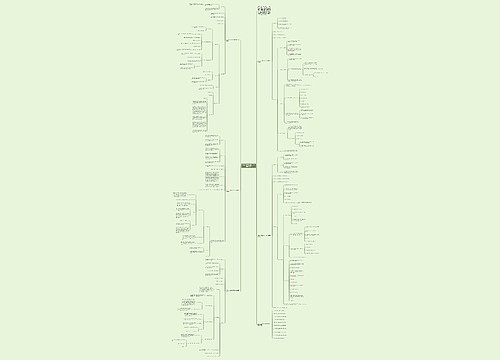
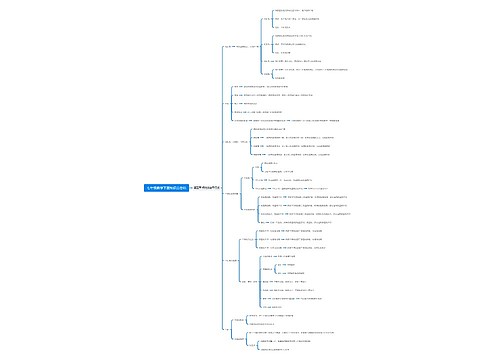
高中数学 排列组合常用方法思维导图
数学老师
2023-03-22

高中数学排列组合常用方法思维导图包含了许多方法和思路:特殊优先法优先安排特殊元素或特殊位置,相邻捆绑法将相邻元素看作一个整体与其他元素一起排列,注意捆绑元素的内部排列,不相邻插空法先考虑不受限制的元素的排列,在将不相邻的元素插在前面元素排列当中,定序除法用于有顺序要求的排列问题,定序排他法可用于有部分顺序排列的问题,直排法将元素分为多排的排列问题,可以看成一排问题,在分段研究,重排求幂法可以用于可以重复的排列问题,实际以元素为研究对象,元素不受位置限制,可以逐一安排各个元素,圆排问题可以先看成直排问题,在除以元素的个数n,间接法可用于正面分类太多的情况,从反面开始入手,分组分配思路是先分组后分配,分组是组合问题,分配是排列问题,完全非均匀分组只需要分组即可,完全均匀分组分组以后除以组数的阶乘,部分均匀分组有m组元素个数相同,则分组后除以m!,在分配问题中,相同元素的分配可用挡板法,将n个相同的元素分成m份,每份至少一个,可以用m-1块隔板,插入n个元素排成一排的n-1个空隙中,所有分法数为,不相同元素的分配遵循分部乘法计数原理,先分组后分配,有限制条件的分配问题应该采用分类求解,数字排序查字典法应该从高位向低位查,依次求出其符合要求的个数,根据分类计数原理求出其总数,而小集团问题则可以先整体后局部。