物理中考复习教案思维导图
泪尽
2023-04-06

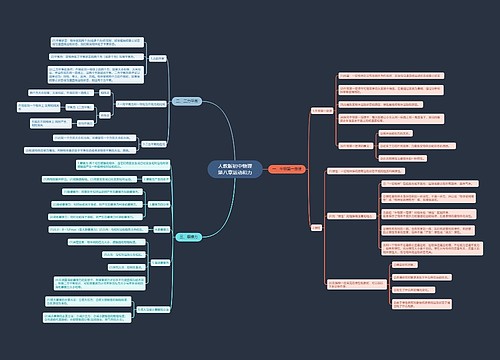
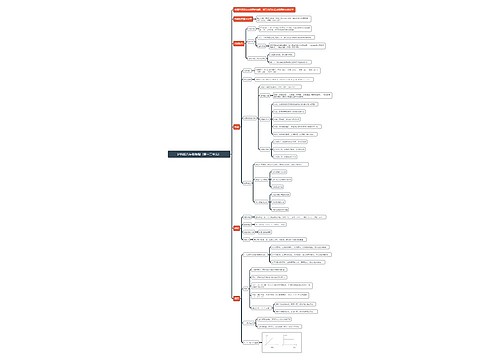
物理中考复习教案
物理
中考
复习
教案
时间如白驹过隙般流逝,我们又将学习新的知识,有新的感受,何不为即将开展的教学工作做一个计划呢?教师应该怎么开展物理教学计划呢?下面是树图网为大家整理的5篇物理中考复习教案内容,感谢大家阅读,希望能对大家
树图思维导图提供《物理中考复习教案》在线思维导图免费制作,点击“编辑”按钮,可对《物理中考复习教案》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6ea6a35e9e8bb41bf17fef438fe4ca5a
思维导图大纲
相关思维导图模版
物理中考复习教案思维导图模板大纲
时间如白驹过隙般流逝,我们又将学习新的知识,有新的感受,何不为即将开展的教学工作做一个计划呢?教师应该怎么开展物理教学计划呢?下面是树图网为大家整理的5篇物理中考复习教案内容,感谢大家阅读,希望能对大家有所帮助!
物理中考复习教案1
《抛体运动的规律》
教学目标
知识与技能
1.理解平抛运动是匀变速运动,其加速度为g.
2.掌握抛体运动的位置与速度的关系.
过程与方法
1.掌握平抛运动的特点,能够运用平抛规律解决有关问题.
2.通过例题分析再次体会平抛运动的规律.
情感、态度与价值观
1.有参与实验总结规律的热情,从而能更方便地解决实际问题.
2.通过实践,巩固自己所学的知识.
教学重难点
教学重点
分析归纳抛体运动的规律
教学难点
应用数学知识分析归纳抛体运动的规律.
教学过程
[新课导入]
上一节我们已经通过实验探究出平抛运动在竖直方向和水平方向上的运动规律,对平抛运动的特点有了感性认识.这一节我们将从理论上对抛体运动的规律作进一步分析,学习和体会在水平面上应用牛顿定律的方法,并通过应用此方法去分析没有感性认识的抛体运动的规律.
[新课教学]
一、抛体的位置
我们以平抛运动为例来研究抛体运动所共同具有的性质.
首先我们来研究初速度为。的平抛运动的位置随时间变化的规律.用手把小球水平抛出,小球从离开手的瞬间(此时速度为v,方向水平)开始,做平抛运动.我们以小球离开手的位置为坐标原点,以水平抛出的方向为x轴的方向,竖直向下的方向为y轴的方向,建立坐标系,并从这一瞬间开始计时.
师:在抛出后的运动过程中,小球受力情况如何?
生:小球只受重力,重力的方向竖直向下,水平方向不受力.
师:那么,小球在水平方向有加速度吗?它将怎样运动?
生:小球在水平方向没有加速度,水平方向的分速度将保持v不变,做匀速直线运动.
师:我们用函数表示小球的水平坐标随时间变化的规律将如何表示?
生:x=vt
师:在竖直方向小球有加速度吗?若有,是多大?它做什么运动?它在竖直方向有初速度吗?
生:在竖直方向,根据牛顿第二定律,小球在重力作用下产生加速度g.做自由落体运动,而在竖直方向上的初速度为0.
师:那根据运动学规律,请大家说出小球在竖直方向的坐标随时间变化的规律.
生:y=1/2gt2
师:小球的位置能否用它的坐标(x,y)描述?能否确定小球在任意时刻t的位置?
生:可以.
师:那么,小球的运动就可以看成是水平和竖直两个方向上运动的合成.t时间内小球合位移是多大?
生:
师:若设s与+x方向(即速度方向)的夹角为θ,如图6.4—1,则其正切值如何求?
生:
[例1]一架飞机水平匀速飞行.从飞机上海隔l s释放一个铁球,先后释放4个,若不计空气阻力,从地面上观察4个小球( )
A.在空中任何时刻总是捧成抛物线,它们的落地点是等间距的
B.在空中任何时刻总是排成抛物线,它们的落地点是不等间距的
C.在空中任何时刻总在飞机正下方,排成竖直的直线,它们的落地点是等间距的
D.在空中任何时刻总在飞机的正下方,捧成竖直的直线,它们的落地点是不等间距的。
解析:因为铁球从飞机上释放后做平抛运动,在水平方向上有与飞机相同的速度.不论铁球何时从飞机上释放,铁球与飞机在水平方向上都无相对运动.铁球同时还做自由落体运动,它在竖直方向将离飞机越来越远.所以4个球在落地前始终处于飞机的正下方,并排成一条直线,又因为从飞机上每隔1s释放1个球,而每个球在空中运动的时间又是相等的,所以这4个球落地的时间也依次相差1 s,它们的落地点必然是等间距的.若以飞机为参考系观察4个铁球都做自由落体运动.此题把曲线运动利用分解的方法"化曲为直",使其成为我们所熟知的直线运动,则据运动的独立性,可以分别在这两个方向上用各自的运动规律研究其运动过程.
二、抛体的速度
师:由于运动的等时性,那么大家能否根据前面的结论得到物体做平抛运动的时间?
生:由y=1/2gt2得到,运动时间
师:这说明了什么问题?
生:这说明了做平抛运动的物体在空中运动的时间仅取决于下落的高度,与初速度无关.
师:那么落地的水平距离是多大?
生:落地的水平距离
师:这说明了什么问题?
生:这说明了平抛运动的水平位移不仅与初速度有关系,还与物体的下落高度有关.
师:利用运动合成的知识,结合图6.4—2,求物体落地速度是多大?结论如何?
生:落地速度,即落地速度也只与初速度v和下落高度h有关.
师:平抛运动的速度与水平方向的夹角为a,一般称为平抛运动的偏角.实际上,常称为平抛运动的偏角公式,在一些问答题中可以直接应用此结论分析解答
[例2]一个物体以l0 m/s的速度从10 m的水平高度抛出,落地时速度与地面的夹角θ是多少(不计空气阻力)?
[例3]在5 m高的地方以6 m/s的初速度水平抛出一个质量是10 kg的物体,则物体落地的速度是多大?从抛出点到落地点发生的位移是多大?(忽略空气阻力,取g=10m/s2)
[交流与讨论]
应用运动的合成与分解的方法我们探究了做平抛运动的物体的位移和速度.请大家根据我们探究的结果研究一下平抛运动的物体位移和速度之间存在什么关系.
参考解答:根据前面的探究结果我们知道,物体的位移,与x轴的夹角的正切值为tanθ=gt/2v.物体的速度,与x轴的夹角的正切值为tanθ=gt/v.可以看到位移和速度的大小没有太直接的关系,但它们的方向与x轴夹角的正切是2倍关系.利用这个关系我们就可以很方便地计算物体速度或位移的方向了. 师:在(2)中,与匀变速直线运动公式vt2=v02+2as,形式上一致的,其物理意义相同吗? 生:物理意义并不相同,在中的h,并不是平抛运动的位移,而是竖直方向上的位移,在
中的s就是表示匀速直线运动的位移.对于平抛运动的位移,是由竖直位移和水平位移合成而得的.
师:平抛运动的轨迹是曲线(抛物线),某一时刻的速度方向即为曲线上物体所在位置的切线方向.设物体运动的时间为t,则这一时刻的速度与竖直方向夹角的正切值tanβ=v0/gt,而物体下落的高度为h==1/2gt2.如图6.4—3.
图中的A点为速度的切线与抛出点的水平线的交点,C点为物体所在位置的竖直线与水平线的交点,从图中可以看出A为水平线段OC的中点.平抛运动的这一重要特征,对我们分析类平抛运动,特别是带电粒子在电场中偏转是很有帮助的.
平抛运动常分解成水平方向和竖直方向的两个分运动来处理,由于竖直分运动是初速度为零的匀加速直线运动,所以初速度为零的匀加速直线运动的公式和特点均可以在此应用.另外,有时候根据具体情况也可以将平抛运动沿其他方向分解.
三、斜抛运动
师:如果物体抛出时的速度不是沿水平方向,而是斜向上方或斜向下方的(这种情况称为斜抛),它的受力情况是什么样的?加速度又如何?
生:它的受力情况与平抛完全相同,即在水平方向仍不受力,加速度仍是0;在竖直方向仍只受重力,加速度仍为g.
师:实际上物体以初速度v沿斜向上或斜向下方抛出,物体只在重力作用下的运动,如何表示?与平抛是否相同?
生:斜抛运动沿水平方向和竖直方向初速度与平抛不同,分别是vx=vcosθ和vy=sinθ.
由于物体运动过程中只受重力,所以水平方向速度vx=vcosθ保持不变,做匀速直线运动;而竖直方向上因受重力作用,有竖直向下的重力加速度J,同时有竖直向上的初速度vy=sinθ,因此做匀减速运动(是竖直上抛运动,当初速度向斜下方,竖直方向的分运动为竖直下抛运动),当速度减小到。时物体上升到点,此时物体由于还受到重力,所以仍有一个向下的加速度g,将开始做竖直向下的加速运动.因此,斜抛运动可以看成是水平方向速度为vx=vcosθ的匀速直线运动和竖直方向初速度为vy=sinθ的竖直上抛或竖直下抛运动的合运动.
师:斜抛运动分斜上抛和斜下抛(由初速度方向确定)两种,下面以斜上抛运动为例讨论.
师:斜抛运动的特点是什么?
生:特点:加速度a=g,方向竖直向下,初速度方向与水平方向成一夹角θ斜向上,θ=90°时为竖直上抛或竖直下抛运动θ=0°时为平抛运动.
师:常见的处理方法:
①将斜上抛运动分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动,这样有由此可以得到哪些特点?
生:由此可得如下特点:a.斜向上运动的时间与斜向下运动的时间相等;b.从轨道点将斜抛运动分为前后两段具有对称性,如同一高度上的两点,速度大小相等,速度方向与水平线的夹角相同.
师:②将斜抛运动分解为沿初速度方向的斜向上的匀速直线运动和自由落体运动两个分运动,用矢量合成法则求解.
③将沿斜面和垂直斜面方向作为x、y轴,分别分解初速度和加速度后用运动学公式解题.
[交流与讨论]
对于斜抛运动我们只介绍下船上抛和斜下抛的研究方法,除了平抛、斜上抛、斜下抛外,抛体运动还包括竖直上抛和竖直下抛,请大家根据我们研究前面几种抛体运动的方法来研究一下竖直上抛和竖直下抛.
参考解答:对于这两种运动来说,它们都是直线运动,但这并不影响用运动的合成与分解的方法来研究它们.这个过程我们可以仿照第一节中我们介绍的匀加速运动的分解过程.对竖直上抛运动,设它的初速度为v0,那么它的速度就可以写成v= v0—gt的形式,位移写成x= v0t—g t2/2的形式.那这样我们就可以进行分解了.把速度写成v1= v0,v2=—gt的形式,把位移写成xl= v0t,x2= —g t2/2的形式,这样我们可以看到,竖直上抛运动被分解成了一个竖直向上的匀速直线运动和一个竖直向上的匀减速运动.对于竖直下抛运动可以采取同样的方法进行处理.
课后小结
1.具有水平速度的物体,只受重力作用时,形成平抛运动.
2.平抛运动可分解为水平匀蓬运动和竖直自由落体运动.平抛位移等于水平位移和竖直位移的矢量和;平抛瞬时速度等于水平速度和竖直速度的矢量和.
3.平抛运动是一种匀变速曲线运动.
4.如果物体受到恒定合外力作用,并且合外力跟初速度垂直,形成类似平抛的匀变速曲线运动,只需把公式中的g换成a,其中a=F合/m.
说明:
1.干抛运动是学生接触到的第一个曲线运动,弄清其成固是基础,水平初速度的获得是同题的关键,可归纳众两种;
(1)物体被水平加速:水平抛出、水干射出、水平冲击等;
(2)物体与原来水平运动的载体脱离,由于惯性而保持原来的水平速度.
2.平抛运动的位移公式和速度公式中有三个含有时间t,应根据不同的已知条件来求时间.但应明确:平抛运动的时间完全由抛出点到落地点的竖直高度确定(在不高的范国内g恒定),与抛出的速度无关.
物理中考复习教案2
《质点在平面内的运动》
教学目标
知识与技能
1.理解平抛运动是加速度为g的匀变速运动,其水平方向是匀速直线运动,竖直方向为自由落体运动.
2.了解斜抛运动及运动的合成与分解的迁移应用.
过程与方法
会用平抛运动的规律解答相关问题,以数学中的抛物线方程及图象为工具建立物理模型,理解抛体运动的规律及处理方法.
情感、态度与价值观
1.体会各学科之间的联系与发展,培养空间想象能力和数学计算能力以及知识方法的应用能力.
2.领略抛体运动的对称与和谐,培养对科学的好奇心和求知欲.
教学重难点
1.知道什么是抛体运动,什么是平抛运动.知道平抛运动是匀变速曲线运动,加速度为g.
2.用运动的分解、合成结合牛顿运动定律研究抛体运动的特点,知道平抛运动可分为水平方向的匀速直线运动和竖直方向的自由落体运动.
3.能应用平抛运动的规律交流讨论并解决实际问题.在得出平抛运动规律的基础上进而分析斜抛运动.掌握研究抛体运动的一般方法.
教学过程
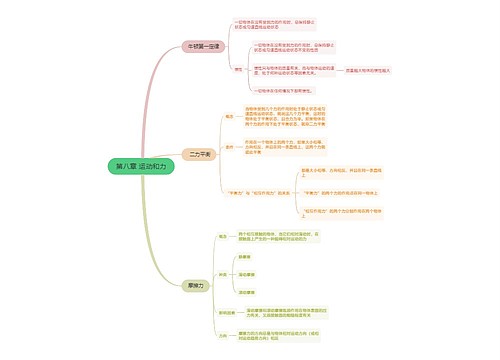
一、抛体运动
探究交流:体育运动中投掷的链球、铅球、铁饼、标枪等(如图所示),都可以看做是抛体运动吗?都可以看成是平抛运动吗?
1.基本知识
(1)定义
以一定的速度将物体抛出,物体只受重力作用的运动.
(2)平抛运动
初速度沿水平方向的抛体运动.
(3)平抛运动的特点
①初速度沿水平方向.②只受重力作用.
2.思考判断
(1)水平抛出的物体所做的运动就是平抛运动.(×)
(2)平抛运动中要考虑空气阻力的作用.(×)
(3)平抛运动的初速度与重力垂直.(√)
二、平抛运动的速度
1.基本知识
将物体以初速度v0水平抛出,由于物体只受重力作用,t时刻的速度为:
(1)水平方向:vx=v0.
(2)竖直方向:vy=gt.
(4)速度变化特点:由于平抛运动的物体只受重力作用,所以其加速度恒为g,因此在平抛运动中速度的变化量Δv=gΔt,由于g是常量,所以任意两个相等的时间间隔内速度的变化量相等,方向竖直向下,即任意两个相等的时间间隔内速度的变化相同,如图所示.
2.思考判断
(1)平抛运动的物体初速度越大,下落得越快.(×)
(2)做平抛运动的物体下落时,速度与水平方向的夹角θ越来越大.(√)
(3)如果下落时间较长,平抛运动的物体的速度方向变为竖直方向.(×)
3.探究交流
平抛运动中,竖直方向的分速度vy=gt,除该公式外,还有求vy的公式吗?
【提示】由于竖直分运动是自由落体运动,所以
例:关于平抛物体的运动,以下说法正确的是()
A.做平抛运动的物体,速度和加速度都随时间的增加而增大
B.做平抛运动的物体仅受到重力的作用,所以加速度保持不变
C.平抛物体的运动是匀变速运动
D.平抛物体的运动是变加速运动
【答案】BC
三、平抛运动的位移
1.基本知识
将物体以初速度v0水平抛出,经时间t物体的位移为:
2.思考判断
(1)平抛运动合位移的方向与合速度的方向一致.(×)
(2)平抛运动合位移的大小等于物体的路程.(×)
(3)平抛运动中,初速度越大,落地时间越长.(×)
3.探究交流
飞机向某灾区投放救灾物资,要使物资准确落到指定地点,是飞到目标正上方投放,还是提前投放?
【提示】物资离开飞机前具有与飞机相同的水平方向的速度,当离开飞机后,由于惯性,它们仍然要保持原有的水平向前的运动速度,另外,物资又受到重力作用,于是物资一方面在水平方向向前运动,另一方面向下加速运动,因此,只有提前投放,才能使物资准确落到指定地方.
4.小结:平抛运动的特点
1.速度特点:平抛运动的速度大小和方向都不断变化,故它是变速运动.
2.轨迹特点:平抛运动的运动轨迹是曲线,故它是曲线运动.
3.加速度特点:平抛运动的加速度为自由落体加速度,恒定不变,故它是匀变速运动.
综上所述,平抛运动的性质为匀变速曲线运动.
例:关于平抛运动,下列说法正确的是()
A.平抛运动是匀变速运动
B.平抛运动是变加速运动
C.任意两段时间内加速度相同
D.任意两段相等时间内速度变化相同
【答案】ACD
四、平抛运动的研究方法和规律
【问题导思】
1.如何研究平抛运动比较简单?
2.平抛运动的合速度、合位移怎么求出?
3.试推导平抛运动的轨迹方程.
1.平抛运动的研究方法
(1)由于平抛运动是匀变速曲线运动,速度、位移的方向时刻发生变化,无法直接应用运动学公式,因此研究平抛运动问题时采用运动分解的方法.
(2)平抛运动一般分解为竖直方向上的自由落体运动和水平方向上的匀速直线运动.
2.平抛运动的规律
(1)分运动
五、平抛运动的几个重要推论
【问题导思】
1.平抛运动的飞行时间与初速度有关吗?
2.平抛运动的落地速度决定于哪些因素?
3.平抛运动的速度偏向角与位移偏向角间的关系如何?
1.平抛运动的时间
A.tan φ=sin θ B.tan φ=cos θ
C.tan φ=tan θ D.tan φ=2tan θ
【答案】D
六、平抛运动的临界问题
例:如图所示,女排比赛时,排球场总长为18 m,设球网高度为2 m,运动员站在网前3 m处正对球网跳起将球水平击出.若击球的高度为2.5 m,为使球既不触网又不越界,求球的速度范围.
2.思考判断
(1)斜抛运动和平抛运动在竖直方向上做的都是自由落体运动.(×)
(2)斜抛运动和平抛运动在水平方向上做的都是匀速直线运动.(√)
(3)斜抛运动和平抛运动的加速度相同.(√)
3.探究交流
对斜上抛运动,有一个点,该点的速度是零吗?为什么
【提示】在斜上抛运动的点,竖直分速度为零.水平分速度等于v0cos θ.故该点的速度v=v0cosθ.
物理中考复习教案3
《曲线运动》
教学目标
【教学目标】
1.知道曲线运动是一种变速运动,它在某点的瞬时速度方向在曲线这一点的切线上。
2.理解物体做曲线运动的条件是所受合外力与初速度不在同一直线上。
3.培养学生观察实验和分析推理的能力。
4.激发学生学习兴趣,培养学生探究物理问题的习惯。
教学重难点
【重点难点】
1.重点:曲线运动的速度方向;物体做曲线运动的条件。
2.难点:物体做曲线运动的条件。
教学过程
【教学过程】
复习提问
前边几章我们研究了直线运动,同学们思考以下两个问题:
1. 什么是直线运动?
2. 物体做直线运动的条件是什么?在实际生活中,普遍发生的是曲线运动,那么什么是曲线运动?本节课我们就来学习这个问题。
新课学习
展示图片: 卫星绕地球的运动人造地球 转弯的火车
这几幅图中物体的运动轨迹有何特点?
( 轨迹是曲线)
请大家举出一些生活中的曲线运动的例子
一、曲线运动的速度方向:
1思考:曲线运动与直线运动除了运动轨迹不同,还有什么区别?2.观察课本P32图6.1-1和图6.1-2
思考:砂轮打磨下来的炽热微粒。飞出去的链球,它们沿着什么方向?
3.讨论或猜测,曲线运动的速度方向应该怎样?
4.是不是象我们大家猜测的这样呢?让我们来看一个演示实验:教师演示课本P32演示实验验证学生的猜测,从而得到结论:
曲线运动速度的方向 :切线方向
5.什么是曲线的切线呢?
结合课本P33图6.1-4阅读课本P33前两段加深曲线的切线的理解。
6.阅读课本P33第四段,试分析推理曲线运动是匀速运动还是变速运动?
速度是________(矢量.标量),所以只要速度方向变化,速度矢量就发生了________,也就具有________, 因此曲线运动是________。
二、物体做曲线运动的条件:
1.提出问题:既然曲线运动是变速运动,那么由
可知具有加速度,又由 可知受力不为零,那到底有什么样的特点呢?
2.实验探究
器材:光滑玻璃板 小钢球 磁铁
演示:小钢球在水平玻璃板上做匀速直线运动。
问题:给你一磁铁,如何使小钢球①加速仍做直线运动。②减速仍做直线运动。③做曲线运动。制定你的实验方案。
实验验证:请两名同学利用他们的方案来进行验证。演示给全体学生。
分析论证:
直线加速: 的方向与 的方向相同
②直线减速: 的方向与 的方向相反
③曲线运动: 的方向与 成一夹角
结论:当物体所受的合力的方向与它的速度方向在同一直线时,物体做直线运动;当物体所受合力的方向与它的速度方向不在同一直线上时,物体就做曲线运动
3.物体做曲线运动的条件:当物体所受合力的方向与它的速度方向不在同一直线上时4.实践应用:
飞机扔炸弹,分析为什么炸弹做曲线运动?
讨论题:结合本节所学与前面知识体系来分类归纳力和运动的关系。
三、小结
同学们根据自身特点,各自进行。曲线运动是轨迹为 的运动.
一、曲线运动的速度方向
1.曲线运动的方向是 的
2.质点在某一点(或某一时刻)的速度方向是在曲线上这一点的
3.曲线运动一定是 运动
二、物体做曲线运动的条件:
运动物体所受合外力的方向跟它的速度方向 上 。
课后习题
课堂练习
1.关于曲线运动,下列判断正确的是()
A.曲线运动的速度大小可能不变
B.曲线运动的速度方向可能不变
C.曲线运动的速度可能不变
D.曲线运动可能是匀变速运动
2.关于曲线运动的条件,以下说法正确的是()
A.物体受变力作用才可能做曲线运动
B.物体受恒力作用也可能做曲线运动
C.物体所受合力为零不可能做曲线运动
D.物体只要受到合外力就一定做曲线运动
3某物体受同一平面内的几个力作用而做匀速直线运动,从某时刻起撤去其中一个力,而其它力不变,则该物体( )
A、一定做匀加速直线运动
B、一定做匀减速直线运动
C、其轨迹可能是曲线
D、其轨迹不可能是直线
4.关于做曲线运动的物体,下列说法正确的是()
A.它所受的合力一定不为零
B.有可能处于平衡状态
C.速度方向一定时刻改变
D.受的合外力方向有可能与速度方向在同一条直线上
参考答案:1.AD2.BC3.C4.AC
物理中考复习教案4
§2—1声音的产生和传播
学习目标:1、知道声音是由振动产生的。
2、知道声音的传播需要介质,知道声音在不同介质的传播
速度不同。
3、能分析一些常见的声现象。
重、难点:(重)1、学生对声音的产生与传播过程的探究。
(难)2、设计探究的实验。
3、声现象的分析、解释。
关键:指导学生分析实验现象、总结结论。
教学过程:
导学达标:
学生观看第一部分录像——各种各样的声音。引入课题:声音是怎样产生和传播的?
1、声音的产生
演示实验:(1)、敲打音叉——音叉振动,发声。
(2)、握住振动的音叉,声音马上停止。
(3)、放一段声音的录像。
指导学生分析归纳,得出结论:
声音是由物体的振动产生的,振动停止,发声停止。
(4)、扩展:录制声音
2、声音的传播:
(1)、得出:固体、气体可以传播声音。
(2)、实验14页图1-4示:得出:真空不能传播声音
指导学生分析归纳,得出结论:
声音的传播需要介质。
固体、液体、气体都能传播声音,真空不能传声。
学生活动:月球上的宇航员如何交谈?
学生活动:如何证明液体可以传声?
(3)、声波:利用录像让学生知道什么是声波?同水波进行对比。
3、声速:不同介质中的声速是不同的。
学生活动:(1)、看15页的表格内容
(2)、声音在固体、液体、气体中的速度谁快?
15℃声音在空气中的速度为340m/s。
学生活动:对着远处的高山喊可以听到回声,为什么在教室里讲话听不回声?
4、回声:声音的反射。<0.1秒<17米
二、小结:
小结本节内容,明确目标,强调重、难点
三、达标练习:
完成物理时习在线中本节内容,因内容较多,可以留一部分作课外练习。
四、课后活动:
动手动脑:1、2、3题。
教学后记:
在课堂上对声音的知识不能扩展太多,这只是声音的第一节课,可降低难点。
要测一测学生的接受情况。
物理中考复习教案5
科学之旅
●教学目标:一、知识目标: 1.学生认识物理是有趣的、有用的。对物理研究及物理应用有初步印象,激发学生的学习兴趣。
2.步了解学好物理应注意的事情。
二、能力目标: 1.过观察和实验,学习初步的探究问题的方法。
2.过本节课的学习,培养初步的观察能力、分析能力。
三、德育目标: 1.发学生对物理的学习兴趣,培养学生热爱科学的精神,发现科学实验带来的乐趣。
2.共同完成的观察及实验中,学会和同伴的协作和配合。
●教学重点:通过观察、讨论、实验,激发学生学习物理的兴趣和愿望。
●教学难点:能从看到的现象中提出问题。
●教学方法:讨论法、实验法、观察法。
●课时安排: 1课时
●教学过程
一、教师自我介绍
二、引入
[师] 从这个学期开始我们学习一门新课——物理。请同学们观看漂亮的章首图,然后听一位同学带感情地朗读配文。
三、进行新课
[师] 科学之旅的第一站,先请同学们观看几个有趣的实验。
[演示] 课本图0.1-1实验 [演示] 课本图0.1-2实验。
教师边演示,边引导学生观察分析实验现象。
教师再演示书本的几个 [想想做做]
1.放大镜看自己的手指纹:是放大的;再用放大镜看窗外的物体:是缩小的。
2.乓球会落下吗?
[师] 以上的这些实验有趣吗?
[板书] 物理是有趣的
[板书] 物理学的研究范围:声、光、热、电、力等现象
[师] 这些现象不仅有趣且都包含一定的科学道理,以后的学习中我们会逐渐弄清楚其中的奥秘。
物理学不仅有趣,而且非常有用:
[板书] 怎样学习物理。
[板书] (1)勤于观察、勤于动手
[板书] (2)勤于思考、重在理解
[板书] (3)联系实际,联系社会
四、小结
物理学是有趣的,有用的。学习物理要用自己的眼睛仔细观察周围的生活,从中发现问题、提出假设、大胆猜想、善于动手、勇于实践,才能最终发现事物的发展规律,才能在"真理的大海"中勇往直前。
五、布置作业(略)
六、板书设计
物理中考复习教案相关文章:
★ 初中物理教案大全
★ 初中生物理教案
★ 初中物理教案范文大全
★ 初中物理教案范文
★ 初中八年级物理教案
★ 中考物理学习方法总结复习备战2021
★ 八年级物理重难点教学设计5篇
★ 初中物理简单机械所有知识点全整理 -
★ 初三物理课程教学计划5篇
查看更多
相似思维导图模版
首页
我的文件
我的团队
个人中心