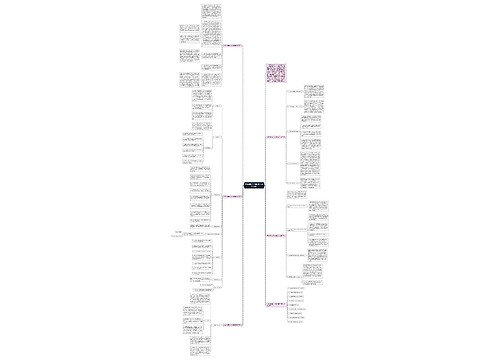
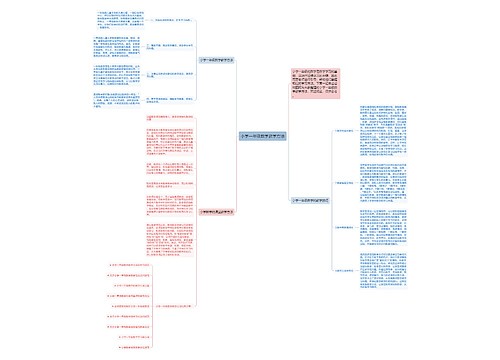
小学一年级数学教学方法及技巧思维导图
补偿
2023-04-04

小学一年级数学教学方法及技巧思维导图培养学生对数学的兴趣,采用数字图书馆备课,课堂巧设计境,联系生活相结合,和生动、风趣、幽默的课堂语言。来提高学生的数学学习热情,教师还可以运用创设情境的方法,让学生融入课堂,与生活实际相结合,让学生更好的理解数学知识和解决实际问题,在应用题教学中,可以用具体的现实情境代替题中内容,变题中的研究对象为学生身边的人和事,引领学生自己发现并解决生活中的数学问题,来帮助学生更好的掌握应用题的解答方法,并提高数学学习效果。
思维导图大纲
相关思维导图模版
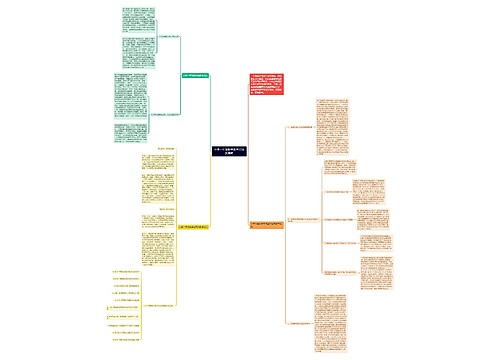
六年级数学有效教学方法及技巧思维导图
 催眠
催眠树图思维导图提供《六年级数学有效教学方法及技巧》在线思维导图免费制作,点击“编辑”按钮,可对《六年级数学有效教学方法及技巧》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:23e78b800ae4d4dc622abf9c77129f11
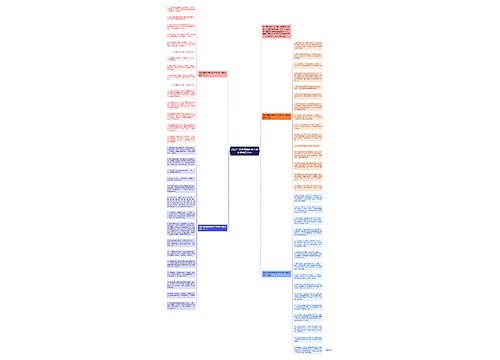
四年级数学下册的教学方法技巧思维导图
 谁相伴
谁相伴树图思维导图提供《四年级数学下册的教学方法技巧》在线思维导图免费制作,点击“编辑”按钮,可对《四年级数学下册的教学方法技巧》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:9d66f46039b784a1923b5b5b7dd9b490