四年级的数学人教版下册教案思维导图
孤街浪徒
2023-04-04

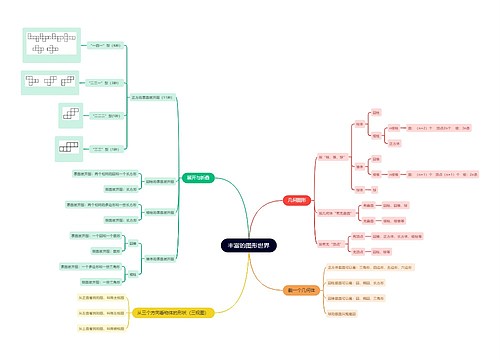
作为一名教育工作者,编写教案是帮助顺利进行教学活动的关键,本模板介绍了四年级数学人教版下册教案的知识点,包含探索乘法的结合律、猜测、举例和验证、运算律的字母描述形式、注重学生已有的经验和认知基础,重点介绍了教学目标、重点和难点,希望能够帮助老师们设计出更好的教学方案,让学生更好的掌握数量关系,提高分析和推理能力,解决实际问题。
思维导图大纲
相关思维导图模版
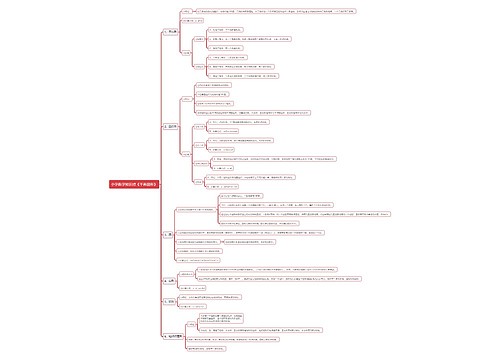
平移人教版数学七年级下册教案思维导图
 余生愿你常欢笑
余生愿你常欢笑树图思维导图提供《平移人教版数学七年级下册教案》在线思维导图免费制作,点击“编辑”按钮,可对《平移人教版数学七年级下册教案》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:50fbedd67dc246a076e34adf33951f0a
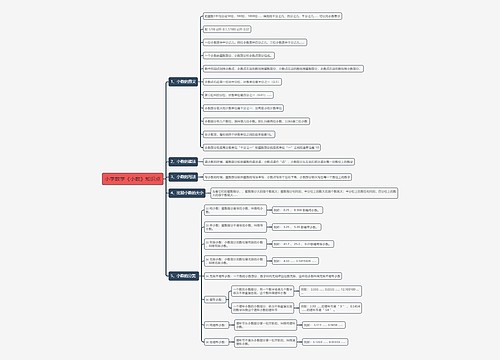
人教版新课标小学数学四年级下册教案范文思维导图
 钻石心
钻石心树图思维导图提供《人教版新课标小学数学四年级下册教案范文》在线思维导图免费制作,点击“编辑”按钮,可对《人教版新课标小学数学四年级下册教案范文》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:d8b8b695237e5dd38bc30ce754e473f4