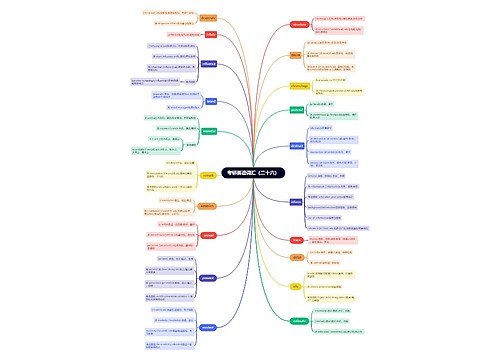
2023应用统计考研核心知识点分析:假设检验思维导图
情书
2023-04-04

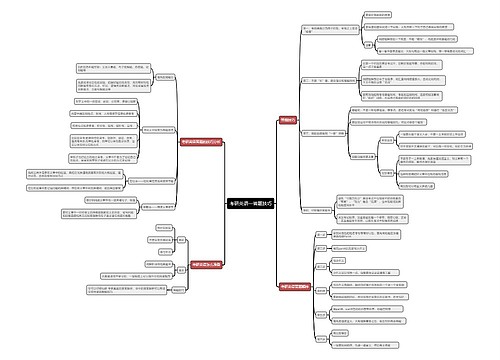
2023考研已经结束了,很多同学想知道应用统计专业考研有哪些核心知识点,树图网已经整理好 2023应用统计考研核心知识点分析:假设检验 的内容,帮助大家了解应用统计专业的核心知识点内容,一起来看看吧! 一、概念 先对总体的参数(或分布形式)提出某种假设,然后利用样本信息判断假设是否成立的过程 有参数检验和非参数检验 逻辑上运用反证法,统计上依据小概率原理 什
树图思维导图提供《2023应用统计考研核心知识点分析:假设检验》在线思维导图免费制作,点击“编辑”按钮,可对《2023应用统计考研核心知识点分析:假设检验》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:73951b3e363de2757831ae76b6b2daef
思维导图大纲
相关思维导图模版
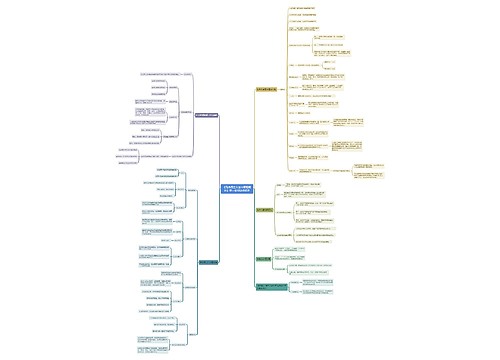
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
 U633687664
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作,点击“编辑”按钮,可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

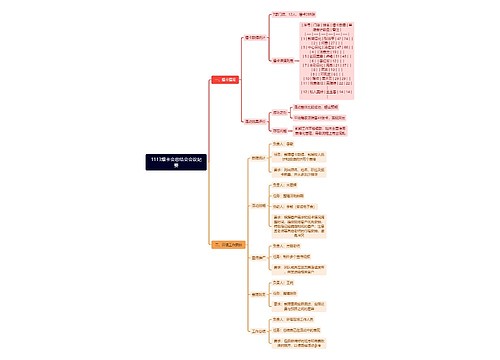
1113爆卡会总结会会议纪要思维导图
 U245265618
U245265618树图思维导图提供《1113爆卡会总结会会议纪要》在线思维导图免费制作,点击“编辑”按钮,可对《1113爆卡会总结会会议纪要》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:aaf6c152a765d5821e8e1787f2b3226e