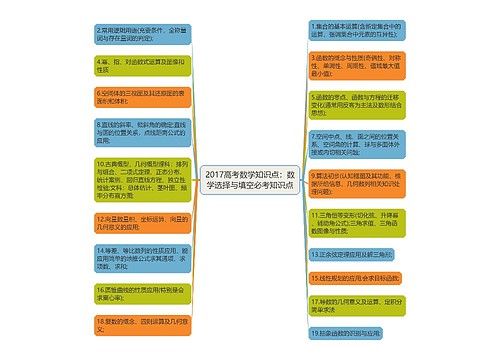
高考数学公式及知识点思维导图

定格苍凉

2023-04-04

浏览量: 9

高考数学公式及知识点

数学公式知识点

高考数学公式及知识点思维导图，包含导数公式、三角函数公式、数学圆锥公式，除了公式，各种几何图形的面积和体积计算公式，和一元二次方程的解、根与系数的关系，还推荐了一些其他相关思维导图模板，供读者参考，通过学习这些公式和知识点，可以有效提高数学成绩，为高考做好充分准备。

思维导图大纲

高三数学知识点之导数公式

1.y=c(c为常数) y'=0

2.y=x^n y'=nx^(n-1)

3.y=a^x y'=a^xlna

y=e^x y'=e^x

4.y=logax y'=logae/x

y=lnx y'=1/x

5.y=sinx y'=cosx

6.y=cosx y'=-sinx

7.y=tanx y'=1/cos^2x

8.y=cotx y'=-1/sin^2x

9.y=arcsinx y'=1/√1-x^2

10.y=arccosx y'=-1/√1-x^2

11.y=arctanx y'=1/1+x^2

12.y=arccotx y'=-1/1+x^2

三角函数公式

锐角三角函数公式

sin α=∠α的对边 / 斜边

cos α=∠α的邻边 / 斜边

tan α=∠α的对边 / ∠α的邻边

cot α=∠α的邻边 / ∠α的对边

倍角公式

Sin2A=2SinA?CosA

Cos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1

tan2A=(2tanA)/(1-tanA^2)

(注：SinA^2 是sinA的平方 sin2(A) )

三倍角公式

sin3α=4sinα·sin(π/3+α)sin(π/3-α)

cos3α=4cosα·cos(π/3+α)cos(π/3-α)

tan3a = tan a · tan(π/3+a)· tan(π/3-a)

三倍角公式推导

sin3a

=sin(2a+a)

=sin2acosa+cos2asina

辅助角公式

Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中

sint=B/(A^2+B^2)^(1/2)

cost=A/(A^2+B^2)^(1/2)

tant=B/A

Asinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t)，tant=A/B

降幂公式

sin^2(α)=(1-cos(2α))/2=versin(2α)/2

cos^2(α)=(1+cos(2α))/2=covers(2α)/2

tan^2(α)=(1-cos(2α))/(1+cos(2α))

推导公式

tanα+cotα=2/sin2α

tanα-cotα=-2cot2α

1+cos2α=2cos^2α

1-cos2α=2sin^2α

1+sinα=(sinα/2+cosα/2)^2

=2sina(1-sin2a)+(1-2sin2a)sina

=3sina-4sin3a

cos3a

=cos(2a+a)

=cos2acosa-sin2asina

=(2cos2a-1)cosa-2(1-sin2a)cosa

=4cos3a-3cosa

sin3a=3sina-4sin3a

=4sina(3/4-sin2a)

=4sina[(√3/2)2-sin2a]

=4sina(sin260°-sin2a)

=4sina(sin60°+sina)(sin60°-sina)

=4sina.2sin[(60+a)/2]cos[(60°-a)/2].2sin[(60°-a)/2]cos[(60°-a)/2]

=4sinasin(60°+a)sin(60°-a)

cos3a=4cos3a-3cosa

=4cosa(cos2a-3/4)

=4cosa[cos2a-(√3/2)2]

=4cosa(cos2a-cos230°)

=4cosa(cosa+cos30°)(cosa-cos30°)

=4cosa.2cos[(a+30°)/2]cos[(a-30°)/2].{-2sin[(a+30°)/2]sin[(a-30°)/2]}

=-4cosasin(a+30°)sin(a-30°)

=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]

=-4cosacos(60°-a)[-cos(60°+a)]

=4cosacos(60°-a)cos(60°+a)

上述两式相比可得

tan3a=tanatan(60°-a)tan(60°+a)

数学圆锥公式知识点

正弦定理a/sinA=b/sinB=c/sinC=2R注：其中R表示三角形的外接圆半径

余弦定理b2=a2+c2-2accosB注：角B是边a和边c的夹角

圆的标准方程(x-a)2+(y-b)2=r2注：(a,b)是圆心坐标

圆的一般方程x2+y2+Dx+Ey+F=0注：D2+E2-4F>0

抛物线标准方程y2=2pxy2=-2px-x2=2pyx2=-2py

直棱柱侧面积S=c.h斜棱柱侧面积S=c'.h

正棱锥侧面积S=1/2c.h'正棱台侧面积S=1/2(c+c')h'

圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi.r2

圆柱侧面积S=c.h=2pi.h圆锥侧面积S=1/2.c.l=pi.r.l

弧长公式l=a.ra是圆心角的弧度数r>0扇形面积公式s=1/2.l.r

锥体体积公式V=1/3.S.H圆锥体体积公式V=1/3.pi.r2h

斜棱柱体积V=S'L注：其中,S'是直截面面积，L是侧棱长

柱体体积公式V=s.h圆柱体V=p.r2h

乘法与因式分a2-b2=(a+b)(a-b)a3+b3=(a+b)(a2-ab+b2)a3-b3=(a-b(a2+ab+b2)

三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b

|a-b|≥|a|-|b|-|a|≤a≤|a|

一元二次方程的解-b+√(b2-4ac)/2a-b-√(b2-4ac)/2a

根与系数的关系X1+X2=-b/aX1.X2=c/a注：韦达定理

判别式

b2-4ac=0注：方程有两个相等的实根

b2-4ac>0注：方程有两个不等的实根

b2-4ac<0注：方程没有实根，有共轭复数根

高考数学公式及知识点相关文章：

★ 高一到高三数学公式和知识点归纳

★ 高考数学必考知识点归纳总结整理2021

★ 高中数学常用公式必备资料

★ 高考数学备考总复习知识点归纳

★ 高考数学必考知识点归纳总结2021

★ 高三最全数学知识点2021

★ 高考数学知识点总结经验分享2021

★ 高考的常考数学知识点总结2021

★ 实用高考数学知识点总结经验分享2021

★ 2021高考数学必考知识点归纳

2019高考数学知识点：导数公式及推导过程思维导图

橘味猫

1.52

树图思维导图提供《2019高考数学知识点：导数公式及推导过程》在线思维导图免费制作，点击“编辑”按钮，可对《2019高考数学知识点：导数公式及推导过程》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：03015c6930e39159677561dac72db6ff

2019高考数学知识点：三角函数的概念及公式思维导图

多情又困苦

1.95

树图思维导图提供《2019高考数学知识点：三角函数的概念及公式》在线思维导图免费制作，点击“编辑”按钮，可对《2019高考数学知识点：三角函数的概念及公式》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：14df9437d60e04c020e5920979742d92

思维导图模板

基础教育

数学

正文

相似思维导图模版

2019高考数学必备知识点：易错点汇总及提分窍门思维导图

2023-04-20 19:24:13

高考文科数学必考知识点思维导图

2023-04-04 16:31:39

2017高考数学知识点：数学选择与填空必考知识点思维导图

思维导图模版推荐

首页

我的文件

我的团队

个人中心