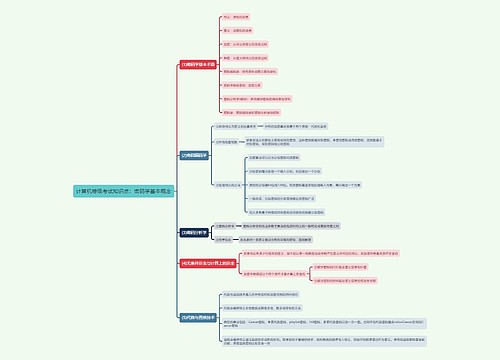
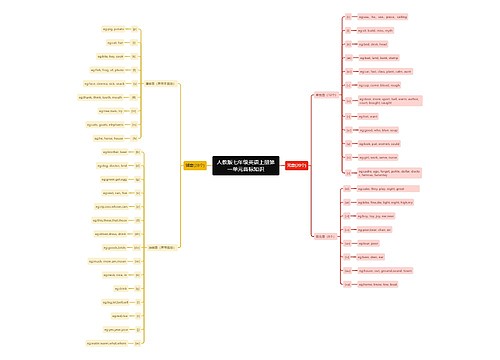
计算机三级PC技术整数的性质和运算思维导图

原来是y

2022-11-13

浏览量: 5

思维导图

考研考证

计算机三级

PC技术

整数的性质和运算

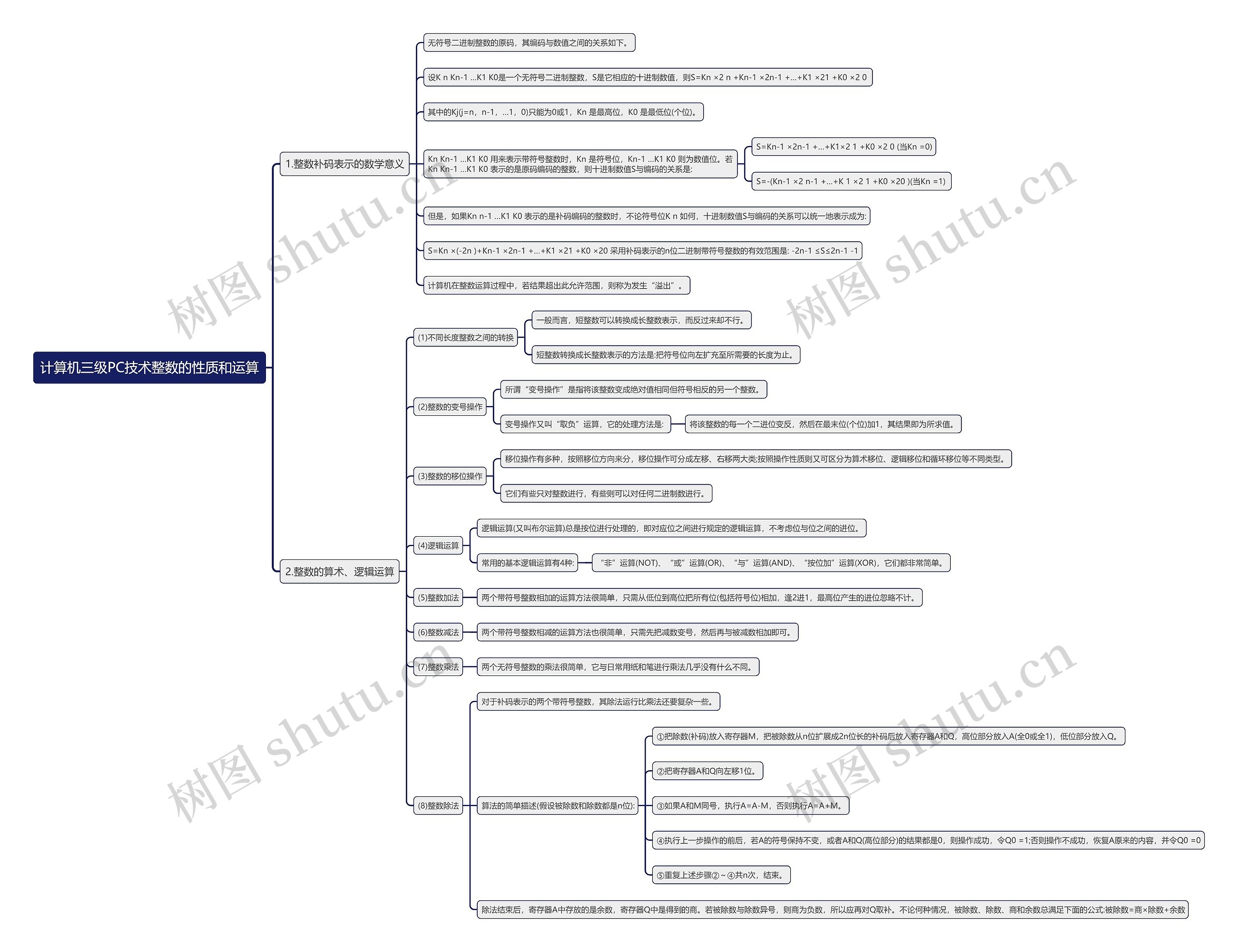
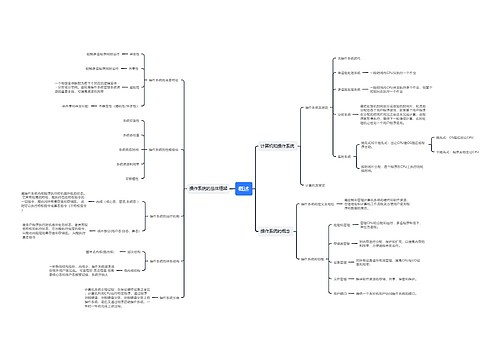
本思维导图主要总结计算机计算机三级考试PC技术知识点整数的性质和运算

树图思维导图提供《计算机三级PC技术整数的性质和运算思维导图》在线思维导图免费制作，点击“编辑”按钮，可对《计算机三级PC技术整数的性质和运算思维导图》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：1c9373a2db4ac549b60966c365d0906a

思维导图大纲

1.整数补码表示的数学意义

无符号二进制整数的原码，其编码与数值之间的关系如下。

设K n Kn-1 …K1 K0是一个无符号二进制整数，S是它相应的十进制数值，则S=Kn ×2 n +Kn-1 ×2n-1 +…+K1 ×21 +K0 ×2 0

其中的Kj(j=n，n-1，…1，0)只能为0或1，Kn 是最高位，K0 是最低位(个位)。

Kn Kn-1 …K1 K0 用来表示带符号整数时，Kn 是符号位，Kn-1 …K1 K0 则为数值位。若Kn Kn-1 …K1 K0 表示的是原码编码的整数，则十进制数值S与编码的关系是:

S=Kn-1 ×2n-1 +…+K1×2 1 +K0 ×2 0 (当Kn =0)

S=-(Kn-1 ×2 n-1 +…+K 1 ×2 1 +K0 ×20 )(当Kn =1)

但是，如果Kn n-1 …K1 K0 表示的是补码编码的整数时，不论符号位K n 如何，十进制数值S与编码的关系可以统一地表示成为:

S=Kn ×(-2n )+Kn-1 ×2n-1 +…+K1 ×21 +K0 ×20 采用补码表示的n位二进制带符号整数的有效范围是: -2n-1 ≤S≤2n-1 -1

计算机在整数运算过程中，若结果超出此允许范围，则称为发生“溢出”。

2.整数的算术、逻辑运算

(1)不同长度整数之间的转换

一般而言，短整数可以转换成长整数表示，而反过来却不行。

短整数转换成长整数表示的方法是:把符号位向左扩充至所需要的长度为止。

(2)整数的变号操作

所谓“变号操作”是指将该整数变成绝对值相同但符号相反的另一个整数。

变号操作又叫“取负”运算，它的处理方法是:

将该整数的每一个二进位变反，然后在最末位(个位)加1，其结果即为所求值。

(3)整数的移位操作

移位操作有多种，按照移位方向来分，移位操作可分成左移、右移两大类;按照操作性质则又可区分为算术移位、逻辑移位和循环移位等不同类型。

它们有些只对整数进行，有些则可以对任何二进制数进行。

(4)逻辑运算

逻辑运算(又叫布尔运算)总是按位进行处理的，即对应位之间进行规定的逻辑运算，不考虑位与位之间的进位。

常用的基本逻辑运算有4种:

“非”运算(NOT)、“或”运算(OR)、“与”运算(AND)、“按位加”运算(XOR)，它们都非常简单。

(5)整数加法

两个带符号整数相加的运算方法很简单，只需从低位到高位把所有位(包括符号位)相加，逢2进1，最高位产生的进位忽略不计。

(6)整数减法

两个带符号整数相减的运算方法也很简单，只需先把减数变号，然后再与被减数相加即可。

(7)整数乘法

两个无符号整数的乘法很简单，它与日常用纸和笔进行乘法几乎没有什么不同。

(8)整数除法

对于补码表示的两个带符号整数，其除法运行比乘法还要复杂一些。

算法的简单描述(假设被除数和除数都是n位):

①把除数(补码)放入寄存器M，把被除数从n位扩展成2n位长的补码后放入寄存器A和Q，高位部分放入A(全0或全1)，低位部分放入Q。

②把寄存器A和Q向左移1位。

③如果A和M同号，执行A=A-M，否则执行A=A+M。

④执行上一步操作的前后，若A的符号保持不变，或者A和Q(高位部分)的结果都是0，则操作成功，令Q0 =1;否则操作不成功，恢复A原来的内容，并令Q0 =0

⑤重复上述步骤②～④共n次，结束。

除法结束后，寄存器A中存放的是余数，寄存器Q中是得到的商。若被除数与除数异号，则商为负数，所以应再对Q取补。不论何种情况，被除数、除数、商和余数总满足下面的公式:被除数=商×除数+余数

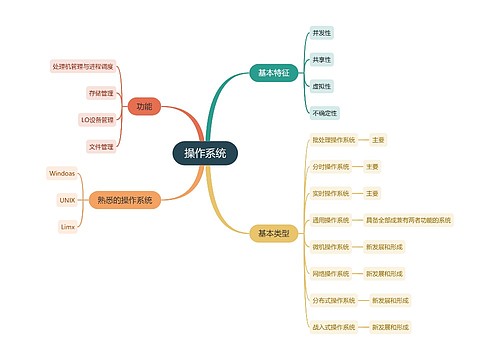
计算机三级PC技术Windows的设备管理思维导图

原来是y

3.05

树图思维导图提供《计算机三级PC技术Windows的设备管理思维导图》在线思维导图免费制作，点击“编辑”按钮，可对《计算机三级PC技术Windows的设备管理思维导图》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：e174e0f882836a70b075436193ffec01

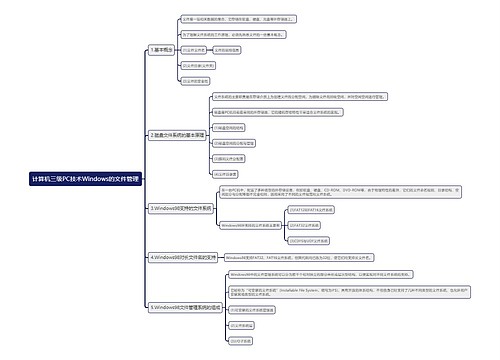
计算机三级PC技术Windows的文件管理思维导图

原来是y

4.5

树图思维导图提供《计算机三级PC技术Windows的文件管理思维导图》在线思维导图免费制作，点击“编辑”按钮，可对《计算机三级PC技术Windows的文件管理思维导图》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：c37ab8bbbb613f63c03dfe38120cc6ab

思维导图模板

资格考试

计算机

正文

相似思维导图模版

计算机等级考试知识点：密码学基本概念思维导图

计算机四级网络工程师知识点TCP/IP的分层思维导图

2022-11-13 13:43:20

思维导图模版推荐

人教版七年级英语上册第一单元音标知识思维导图

首页

我的文件

我的团队

个人中心

计算机三级PC技术整数的性质和运算思维导图

思维导图大纲

相关思维导图模版

1.整数补码表示的数学意义

2.整数的算术、逻辑运算

相似思维导图模版

思维导图模版推荐