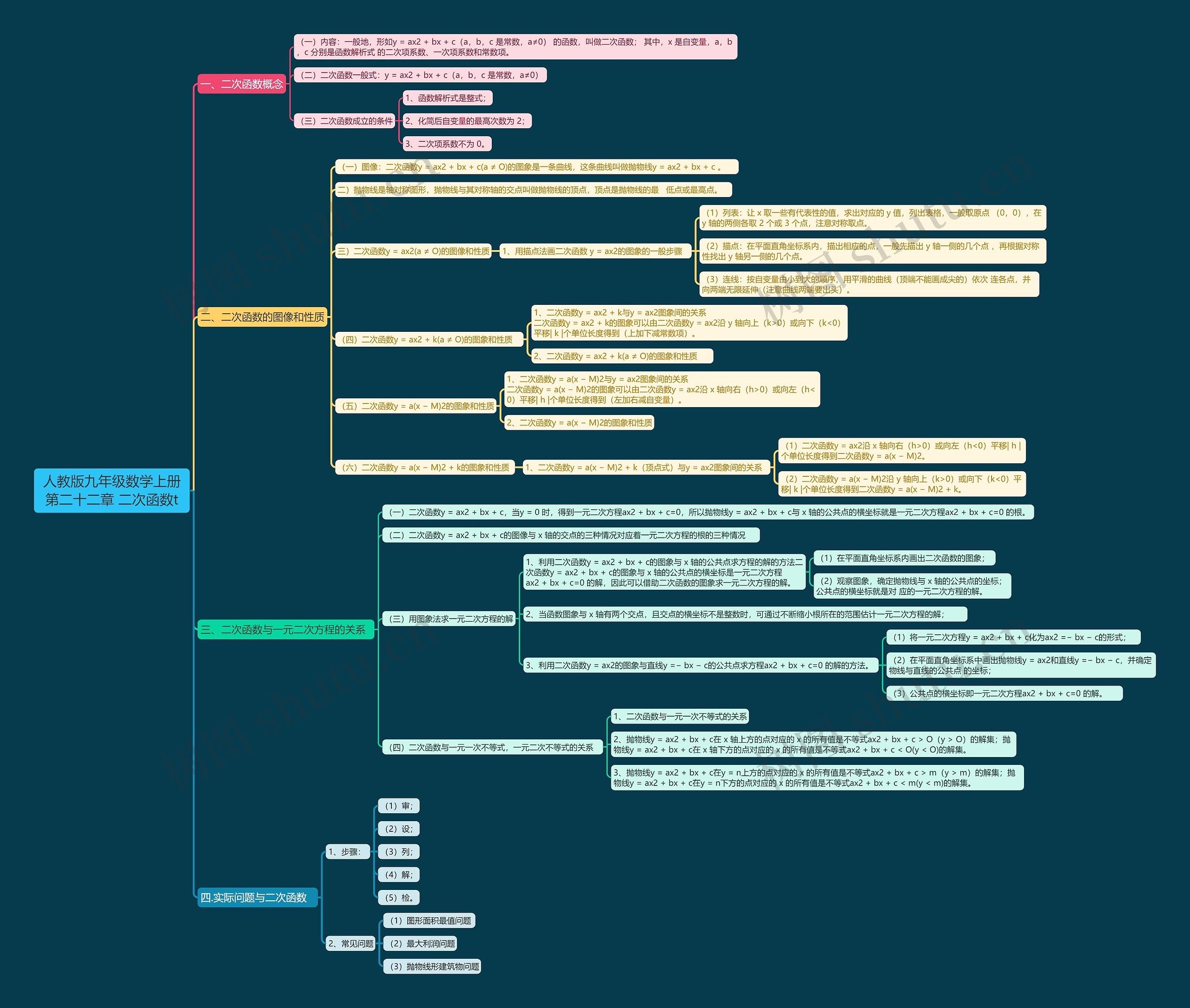
(一)图像:二次函数y = ax2 + bx + c(a ≠ O)的图象是一条曲线,这条曲线叫做抛物线y = ax2 + bx + c 。
二)抛物线是轴对称图形,抛物线与其对称轴的交点叫做抛物线的顶点,顶点是抛物线的最 低点或最高点。
三)二次函数y = ax2(a ≠ O)的图像和性质
1、用描点法画二次函数 y = ax2的图象的一般步骤
(1)列表:让 x 取一些有代表性的值,求出对应的 y 值,列出表格,一般取原点
(0,0),在
y 轴的两侧各取 2 个或 3 个点,注意对称取点。
(2)描点:在平面直角坐标系内,描出相应的点,一般先描出 y 轴一侧的几个点
,再根据对称性找出 y 轴另一侧的几个点。
(3)连线:按自变量由小到大的顺序,用平滑的曲线(顶端不能画成尖的)依次
连各点,并 向两端无限延伸(注意曲线两端要出头)。
(四)二次函数y = ax2 + k(a ≠ O)的图象和性质
1、二次函数y = ax2 + k与y = ax2图象间的关系
二次函数y = ax2 + k的图象可以由二次函数y = ax2沿 y 轴向上(k>0)或向下(k<0)平移| k
|个单位长度得到(上加下减常数项)。
2、二次函数y = ax2 + k(a ≠ O)的图象和性质
(五)二次函数y = a(x − M)2的图象和性质
1、二次函数y = a(x − M)2与y = ax2图象间的关系
二次函数y = a(x − M)2的图象可以由二次函数y = ax2沿 x 轴向右(h>0)或向左(h<0)平移| h |个单位长度得到(左加右减自变量)。
2、二次函数y = a(x − M)2的图象和性质
(六)二次函数y = a(x − M)2 + k的图象和性质
1、二次函数y = a(x − M)2 + k(顶点式)与y = ax2图象间的关系
(1)二次函数y = ax2沿 x 轴向右(h>0)或向左(h<0)平移| h |个单位长度得到二次函数y = a(x − M)2。
(2)二次函数y = a(x − M)2沿 y 轴向上(k>0)或向下(k<0)平移| k |个单位长度得到二次函数y = a(x − M)2 + k。