人教版九年级数学上册第二十一章一元二次方程思维导图

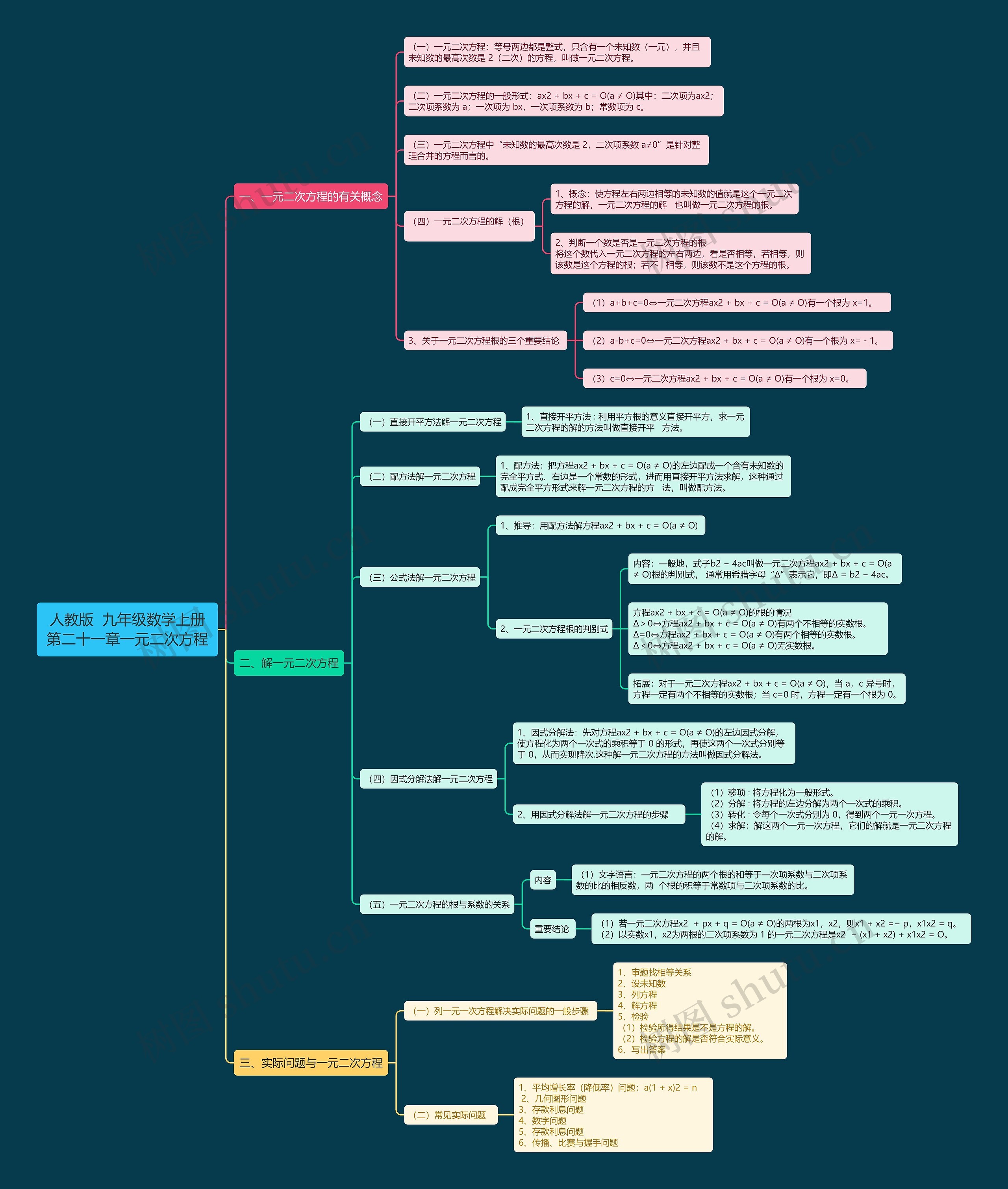
人教版九年级数学上册第二十一章一元二次方程思维导图包含一元二次方程的有关概念，如定义、一般形式和未知数的最高次数，掌握解一元二次方程的方法，如直接开平方法、配方法和公式法，了解一元二次方程根的判别式根的情况，包含两个不相等的实数根、两个相等的实数根和无实数根，对于解方程和解题有很大的帮助。