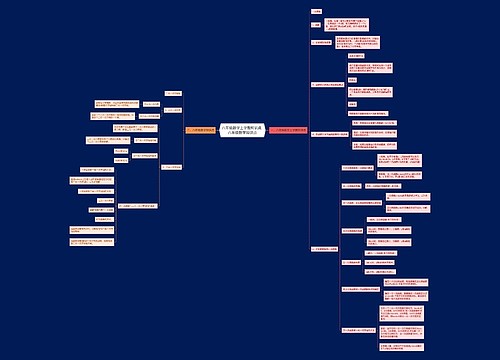
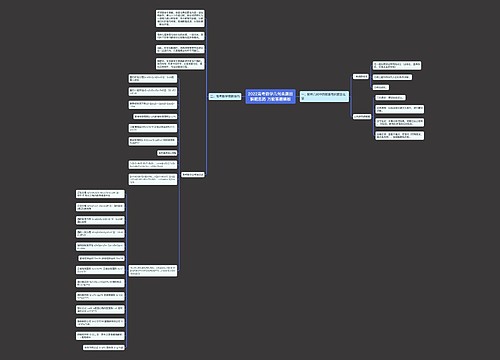
人教版八年级数学上册第十四章 整式的乘法与因式分解思维导图

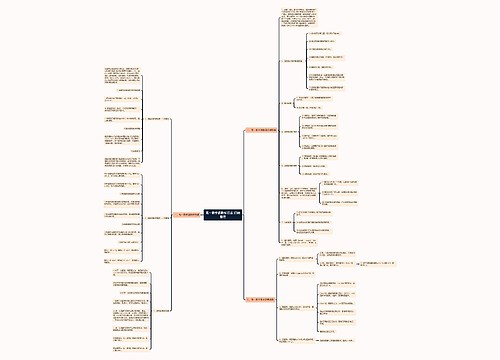
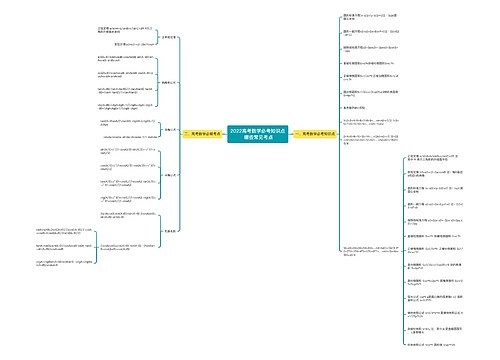
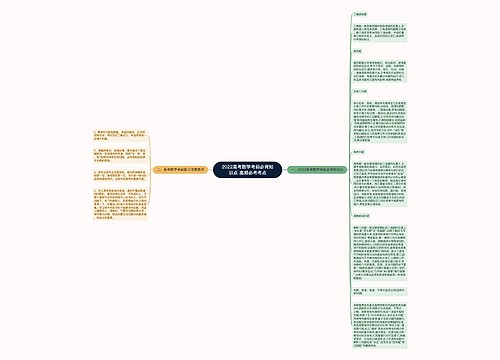
人教版八年级数学上册第十四章整式的乘法与因式分解思维导图提供了整式乘法、同底数幂的乘法、幂的乘方、积的乘方、同底数幂相除、单项式乘以单项式、单项式乘以多项式、多项式乘以多项式、单项式除以单项式、多项式除以单项式、乘法公式、平方差公式、完全平方公式、因式分解。其中因式分解的方法有提取公因式法、运用公式法、十字相乘法和分组分解法，对任意多项式分解因式，首先考虑提取公因式，还需要注意必须分解到每个多项式因式不能在分解为止。