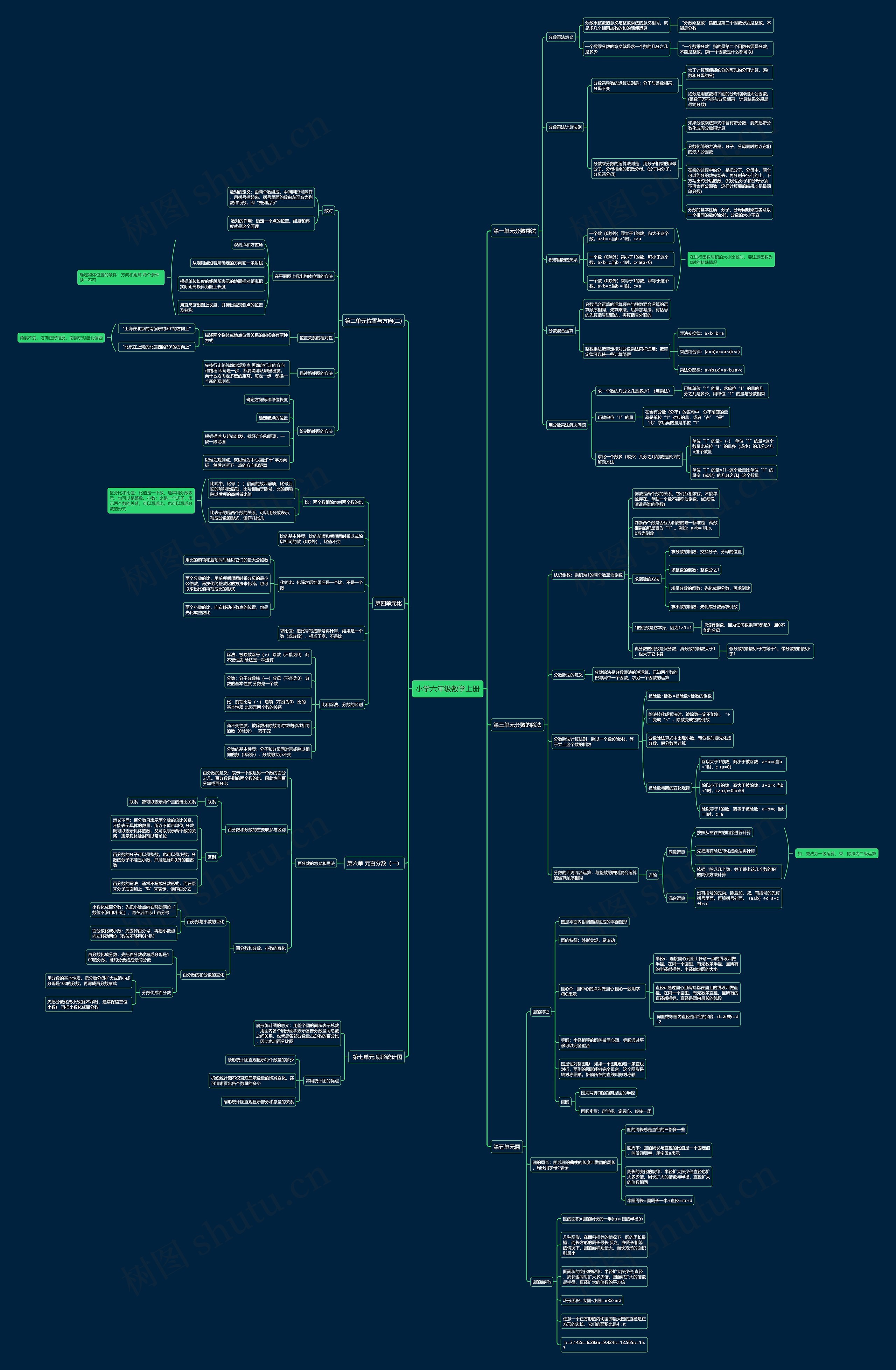
小学六年级数学上册思维导图模板大纲
第一单元分数乘法
分数乘法意义
分数乘整数的意义与整数乘法的意义相同,就
是求几个相同加数的和的简便运算
“分数乘整数”指的是第二个因数必须是整数,不能是分数
一个数乘分数的意义就是求一个数的几分之几是多少
“一个数乘分数”指的是第二个因数必须是分数,不能是整数。(第一个因数是什么都可以)
分数乘法计算法则
分数乘整数的运算法则是:分子与整数相乘,分母不变
为了计算简便能约分的可先约分再计算。(整数和分母约分)
约分是用整数和下面的分母约掉最大公因数。(整数千万不能与分母相乘,计算结果必须是最简分数)
分数乘分数的运算法则是:用分子相乘的积做分子,分母相乘的积做分母。(分子乘分子,分母乘分母)
如果分数乘法算式中含有带分数,要先把带分数化成假分数再计算
分数化简的方法是:分子、分母同时除以它们的最大公因数
在乘的过程中约分,是把分子、分母中,两个可以约分的数先划去,再分别在它们的上、下方写出约分后的数。(约分后分子和分母必须不再含有公因数,这样计算后的结果才是最简单分数)
分数的基本性质:分子、分母同时乘或者除以一个相同的数(0除外),分数的大小不变
积与因数的关系
一个数(0除外)乘大于1的数,积大于这个数。a×b=c,当b >1时,c>a
一个数(0除外)乘小于1的数,积小于这个数。a×b=c,当b <1时,c<a(b≠0)
一个数(0除外)乘等于1的数,积等于这个数。a×b=c,当b =1时,c=a
分数混合运算
分数混合运算的运算顺序与整数混合运算的运算顺序相同,先算乘法,后算加减法,有括号的先算括号里面的,再算括号外面的
整数乘法运算定律对分数乘法同样适用;运算定律可以使一些计算简便
用分数乘法解决问题
求一个数的几分之几是多少?(用乘法)
已知单位“1”的量,求单位“1”的量的几分之几是多少,用单位“1”的量与分数相乘
巧找单位“1”的量
在含有分数(分率)的语句中,分率前面的量就是单位“1”对应的量,或者“占”“是”“比”字后面的量是单位“1”
求比一个数多(或少)几分之几的数是多少的解题方法
单位“1”的量+(-) 单位“1”的量×这个数量比单位“1”的量多(或少)的几分之几=这个数量
单位“1”的量×[1+这个数量比单位“1”的量多(或少)的几分之几]=这个数量
第二单元位置与方向(二)
数对
数对的定义:由两个数组成,中间用逗号隔开
,用括号括起来。括号里面的数由左至右为列数和行数,即“先列后行”
数对的作用:确定一个点的位置。经度和纬度就是这个原理
在平面图上标出物体位置的方法
根据单位长度的线段所表示的地面相对距离把实际距离换算为图上长度
描述路线图的方法
先按行走路线确定观测点,再确定行走的方向和路程.即每走一步,都要说清从哪里出发,向什么方向走多远的距离。每走一步,都换一个新的观测点
绘制路线图的方法
根据描述,从起点出发,找好方向和距离,一段一段地画
以谁为观测点,就以谁为中心画出"十"字方向标,然后判断下一点的方向和距离
第三单元分数的除法
认识倒数:乘积为1的两个数互为倒数
倒数是两个数的关系,它们互相依存,不能单独存在。单独一个数不能称为倒数。(必须说清谁是谁的倒数)
判断两个数是否互为倒数的唯一标准是:两数相乘的积是否为“1”。例如:a×b=1则a、b互为倒数
1的倒数是它本身,因为1×1=1
0没有倒数,因为任何数乘0积都是0,且0不能作分母
真分数的倒数是假分数,真分数的倒数大于1,也大于它本身
分数除法的意义
分数除法是分数乘法的逆运算,已知两个数的积与其中一个因数,求另一个因数的运算
分数除法计算法则:除以一个数(0除外),等于乘上这个数的倒数
除法转化成乘法时,被除数一定不能变,“÷”变成“×”,除数变成它的倒数
分数除法算式中出现小数、带分数时要先化成分数、假分数再计算
被除数与商的变化规律
除以大于1的数,商小于被除数:a÷b=c当b>1时,c(a≠0)
除以小于1的数,商大于被除数:a÷b=c 当b<1时,c>a (a≠0 b≠0)
除以等于1的数,商等于被除数:a÷b=c 当b=1时,c=a
分数的四则混合运算:与整数的四则混合运算的运算顺序相同
连除
同级运算
依据“除以几个数,等于乘上这几个数的积”的简便方法计算
混合运算
没有括号的先乘、除后加、减,有括号的先算括号里面,再算括号外面。(a±b)÷c=a÷c±b÷c
第四单元比
比:两个数相除也叫两个数的比
比式中,比号(∶)前面的数叫前项,比号后面的项叫做后项,比号相当于除号,比的前项除以后项的商叫做比值
比表示的是两个数的关系,可以用分数表示,写成分数的形式,读作几比几
比的基本性质:比的前项和后项同时乘以或除以相同的数(0除外),比值不变
化简比:化简之后结果还是一个比,不是一个数
两个分数的比,用前项后项同时乘分母的最小
公倍数,再按化简整数比的方法来化简。也可
以求出比值再写成比的形式
两个小数的比,向右移动小数点的位置,也是先化成整数比
求比值:把比号写成除号再计算,结果是一个数(或分数),相当于商,不是比
比和除法、分数的区别
除法:被除数除号(÷) 除数(不能为0) 商不变性质 除法是一种运算
分数:分子分数线(—)分母(不能为0) 分数的基本性质 分数是一个数
比:前项比号(∶) 后项(不能为0) 比的基本性质 比表示两个数的关系
商不变性质:被除数和除数同时乘或除以相同的数(0除外),商不变
分数的基本性质:分子和分母同时乘或除以相同的数(0除外),分数的大小不变
第六单 元百分数(一)
百分数的意义和写法
百分数的意义:表示一个数是另一个数的百分之几。百分数是指的两个数的比,因此也叫百分率或百分比
百分数和分数的主要联系与区别
区别
意义不同:百分数只表示两个数的倍比关系,
不能表示具体的数量,所以不能带单位;
分数既可以表示具体的数,又可以表示两个数的关系,表示具体数时可以带单位
百分数的分子可以是整数,也可以是小数;分数的分子不能是小数,只能是除0以外的自然数
百分数的写法:通常不写成分数形式,而在原来分子后面加上“%”来表示,读作百分之
百分数和分数、小数的互化
百分数与小数的互化
小数化成百分数:先把小数点向右移动两位(数位不够用0补足),再在后面添上百分号
百分数化成小数:先去掉百分号,再把小数点向左移动两位(数位不够用0补足)
百分数的和分数的互化
百分数化成分数:先把百分数改写成分母是100的分数,能约分要约成最简分数
分数化成百分数
用分数的基本性质,把分数分母扩大或缩小成分母是100的分数,再写成百分数形式
先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数
第七单元:扇形统计图
扇形统计图的意义:用整个圆的面积表示总数,用圆内各个扇形面积表示各部分数量同总数之间关系,也就是各部分数量占总数的百分比,因此也叫百分比图
常用统计图的优点
折线统计图不仅直观显示数量的增减变化,还可清晰看出各个数量的多少
第五单元圆
圆的特征
圆心O:圆中心的点叫做圆心.圆心一般用字母O表示
半径r:连接圆心到圆上任意一点的线段叫做半径。在同一个圆里,有无数条半径,且所有的半径都相等。半径确定圆的大小
直径d:通过圆心且两端都在圆上的线段叫做直径。在同一个圆里,有无数条直径,且所有的直径都相等。直径是圆内最长的线段
同圆或等圆内直径是半径的2倍:d=2r或r=d÷2
等圆:半径相等的圆叫做同心圆,等圆通过平移可以完全重合
圆是轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。折痕所在的直线叫做对称轴
圆的周长:围成圆的曲线的长度叫做圆的周长,周长用字母C表示
圆周率:圆的周长与直径的比值是一个固定值,叫做圆周率,用字母π表示
周长的变化的规律:半径扩大多少倍直径也扩大多少倍,周长扩大的倍数与半径、直径扩大的倍数相同
圆的面积s
几种图形,在面积相等的情况下,圆的周长最短,而长方形的周长最长;反之,在周长相等的情况下,圆的面积则最大,而长方形的面积则最小
圆面积的变化的规律:半径扩大多少倍,直径、周长也同时扩大多少倍,圆面积扩大的倍数是半径、直径扩大的倍数的平方倍
任意一个正方形的内切圆即最大圆的直径是正方形的边长,它们的面积比是4∶π
π=3.142π=6.283π=9.424π=12.565π=15.7
在进行因数与积的大小比较时,要注意因数为0时的特殊情况思维导图模板大纲
确定物体位置的条件:方向和距离,两个条件缺一不可思维导图模板大纲
角度不变,方向正好相反。南偏东对应北偏西思维导图模板大纲
加、减法为一级运算,乘、除法为二级运算思维导图模板大纲
区分比和比值:比值是一个数,通常用分数表
示,也可以是整数、小数;比是一个式子,表示两个数的关系,可以写成比,也可以写成分数的形式思维导图模板大纲