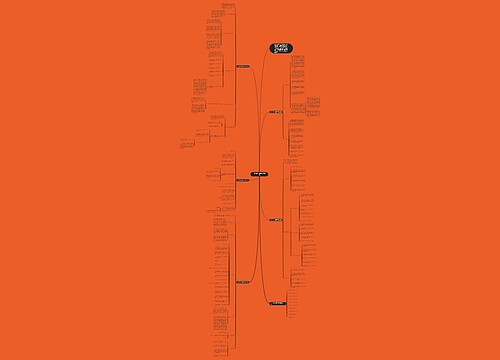
在数学解题需要经历哪些思维过程思维导图

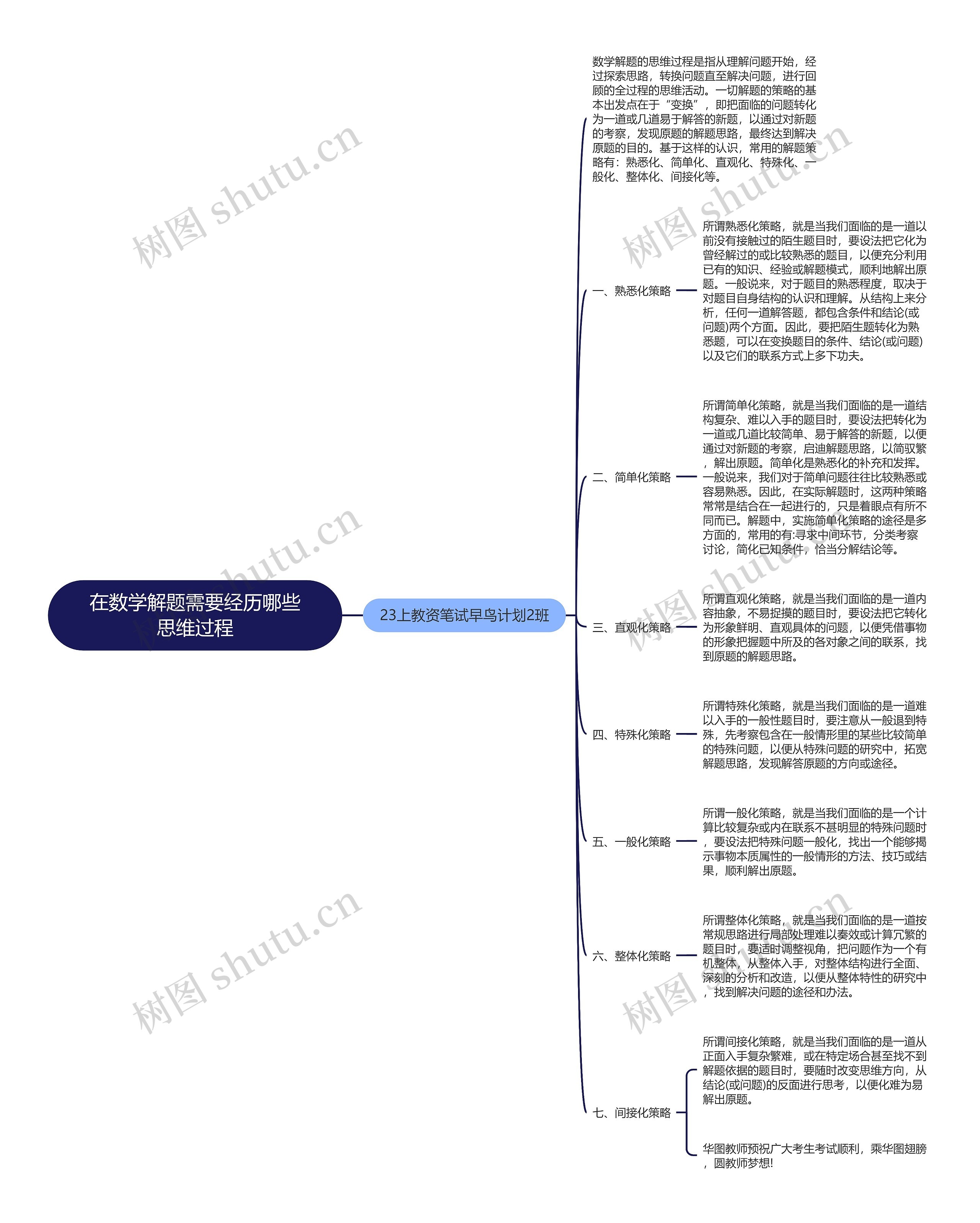
在数学解题中，需要经历一系列思维过程，而思维导图可以帮助我们更好的理清这些过程，解题策略的出发点在于“变换”，即把难题变换为易于解答的新题，通过对新题的考察，去发现原题的解题思路，常用的解题策略有熟悉化、简单化、直观化、特殊化、一般化、整体化。熟悉化策略是为了把陌生的题转化为熟悉的题让我们更好的利用已有的知识和经验，简单化策略是为了把复杂难懂的题目转化为几道简单易答的题目，以简驭繁，直观化策略是为了在面对抽象难懂的题目时，把他转化为形象鲜明、直观具体的问题，更好的找出题目中的联系与规律。特殊化策略则是要从一般性退到特殊化，而一般化策略则相反，要从特殊问题一般化，找出一个能够揭示问题本质属性的一般情形的方法、技巧或结果来解决问题。整体化策略则适用于指那些按常规思路进行处理难以奏效或计算冗繁的题目，需要从整体结构进行、深刻的分析和改造，以便找到解决问题的途径和办法。