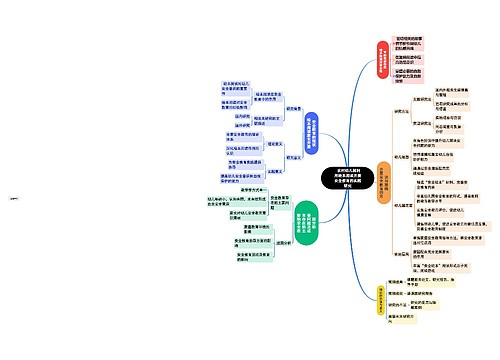
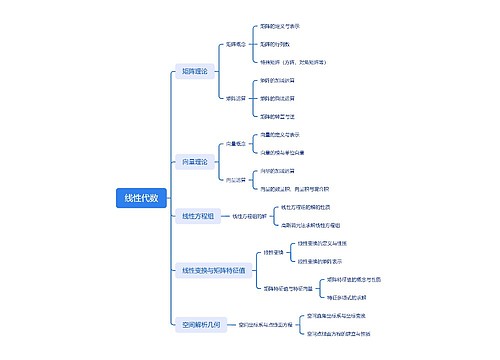
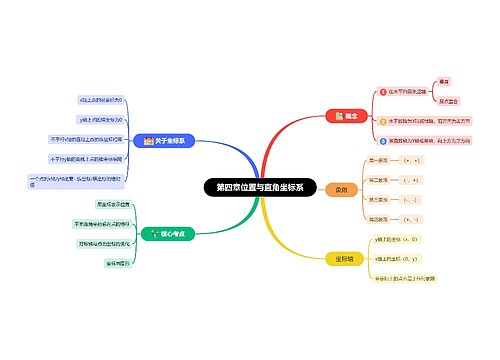
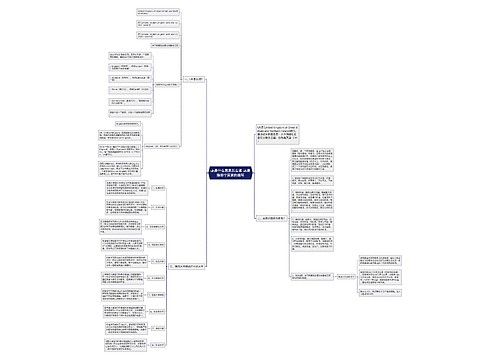
证明三角形内角判定方法 证明三角形内角判定定理思维导图
心不动则不痛
2023-01-12
将一个三角形的三个角分别往内折,三个角刚好组成一平角,平角为180度，所以三角形内角和为180度。下面小编给大家带来证明三角形内角方法，希望能帮助到大家!
树图思维导图提供《证明三角形内角判定方法 证明三角形内角判定定理》在线思维导图免费制作，点击“编辑”按钮，可对《证明三角形内角判定方法 证明三角形内角判定定理》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：f478d67fbade46f6f838289d87eab9ad
思维导图大纲
相关思维导图模版
抓住重点思维导图
~漫埗陽茪~树图思维导图提供《抓住重点》在线思维导图免费制作，点击“编辑”按钮，可对《抓住重点》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：4c49e4799ddf94a339c56e46eb96a826
农村幼儿园利用绘本阅读开展安全教育的实践研究_副本思维导图
U382062580树图思维导图提供《 农村幼儿园利用绘本阅读开展安全教育的实践研究_副本》在线思维导图免费制作，点击“编辑”按钮，可对《 农村幼儿园利用绘本阅读开展安全教育的实践研究_副本》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：2000927dcd222b18fa95af52d1709af8
