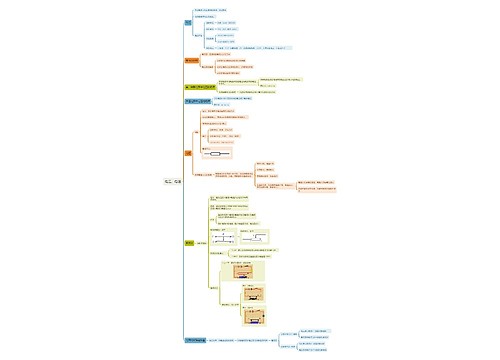
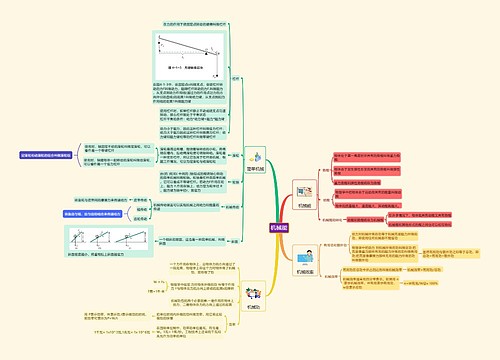
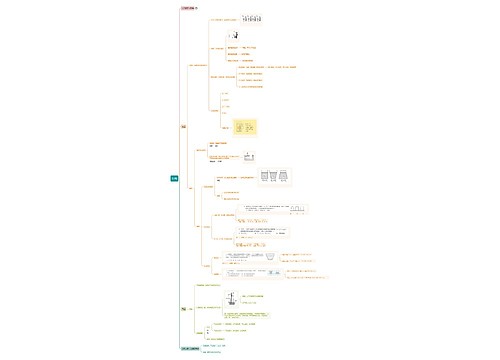
合外力做的功,等于物体动能的改变量,这就是动能定理的内容。动能定理还可以表述为:过程中所有分力做的功的代数和,等于动能的改变量。
功虽然是标量,但有正负一说。最为严谨的公式是第二个公式;最常用的,有些难度的却是第三个公式。
我们来推导动能定理,很多学生可能认为这是没有必要的,其实恰恰相反。
近几年的高考物理试题,特别注重基础知识的推导和与应用。理解各个知识点之间的关联,能够帮你更好的理解物理考点。
在内心理解了动能定理,知道了它的本源,才能在考试中科学运用动能定理来解题。动能定理的推导分为如下两步:
由匀变速直线运动的公式:2as=v2-v02;方程的两边都乘以m,除以2,有:
mas=½mv2-v02=Ek2-Ek1=ΔEk;
运用微积分的思想,我们普通运动模式进行拆分,将其肢解为非常小的一段一段的运动微元法应用;请同学们思考下位移公式的推导过程。
当我们的运动模式被无限分割后,每一小段都可以认为是匀变加速直线运动模式要么a>0;要么a<0;要么a=0。
对任何一段从t=m到t=n,我们都可以利用1中的推理过程得到W=F合s=man=En-Em
W总=W1+W2+W3+……=ma1+ma2+ma3+……=E2-E1+E3-E2+E4-E3+……+En-Em+……=E末-E初
即,W总=E末-E初;这就是普通的直线运动模式下的动能定理推导过程。
曲线运动模式下,动能定理也是成立的,其推导过程不再这里分析,有兴趣的同学可以自己去研究下。
无论是研究外力做的功,还是求物体动能的变化,除了最基本的定义外,我们有了另一条求解途径。
我们在分析复杂运动模式时,除了牛顿动力学内容外,还可以借助于动能定理,避开中间复杂的求加速度等过程。
动能定理和其他知识点的联系太多了。比如,圆周运动的问题,竖直面内从最低点到点的运动,就是要借助动能定理来求解的。
复杂的两个或三个物体,在摩擦力下的运动,有时候用牛顿定律求解很不好求,用牛顿定律+动能定理联合求解,往往会变得简单。
动能定理还会与静电场的问题结合起来,比如求解库仑力做功的问题,因为是变力做功,没有办法直接根据功的定义求解,所以往往是通过动能定理来计算的。
与电磁感应结合,也是动能定理常见的考题。这种情况下往往是研究导体棒运动,在摩擦力、安培力、外界拉力下导体棒动能的变化问题。
如果你仔细分析,你还会发现,爱因斯坦的光电效应方程,与动能定理也非常的近似,或者是动能定理方程的在光学中的推广。
总之,动能定理这个考点太灵活了,几何可以和任意的一个章节结合在一起命题。所以从力学能量开始,任何一个章节遇到复杂的功能关系的问题,同学们要有意识的思考动能定理能不能应用。
1确定研究对象和研究过程。动能定理的研究对象只能是单个物体,如果是系统,那么系统内的物体间不能有相对运动。原因是这时系统内所有内力做的总功不一定是零,会产生或释放其他形式的能量。
2对研究对象进行受力分析。研究对象以外的物体施于研究对象的力都要分析,含重力。
3写出该过程中合外力做的功,或分别写出各个力做的功注意功的正负。如果研究过程中物体受力情况有变化,要分别写出该力在各个阶段做的功。
1动能定理内的物理表达量都是标量式,当合外力对物体做正功时,Ek2>Ek1物体的动能增加;反之则Ek1>Ek2,物体的动能减少;
2动能定理研究的对象应为单一的物体,或者可以当做整体的物体系;如果不是一个整体,那么就有矛盾:到底分析哪个物体所受到的合外力?研究哪个物体的始末态动能?
3动能定理的计算式一般以地面为参考系;各个速度都是以地面为参考系的不能代入相对速度。
4动能定理适用于直线运动,也可使用于曲线运动;适用于恒力合外力做功,也适用于变力做功;力可以分段作用,也可以同时作用,求出各个力所做功的正负代数和即可,这就是动能定理相对牛顿动力学的优越性。
5动能定理的合外力是物体所有的外力之和,在列式计算的时候,画出受力图来,列公式时不要丢力。
1动能定理的研究对象是单独一个物体,机械能守恒定律的研究对象一般是多个物体构成的系统;也可以是一个物体。
2动能定理公式等号的左侧是合外力所做的功,右侧是动能的改变量;是功和能之间的联系。机械能守恒定律公式等号的左侧是一种状态的机械能之和,右侧是另一种状态的机械能之和;是能量不变的方程。
1都可以不去分析具体的加速度、时间来研究能量的变化。

 U633687664
U633687664
 U582679646
U582679646