人教版高一年级数学知识点复习思维导图
心不动则不痛
2022-12-21

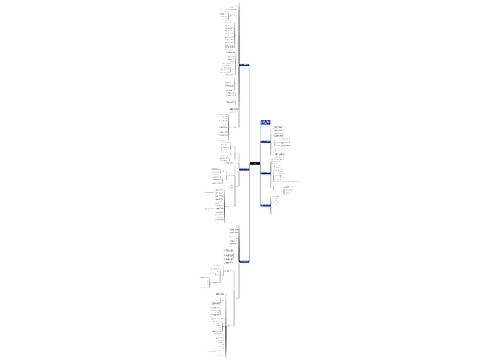
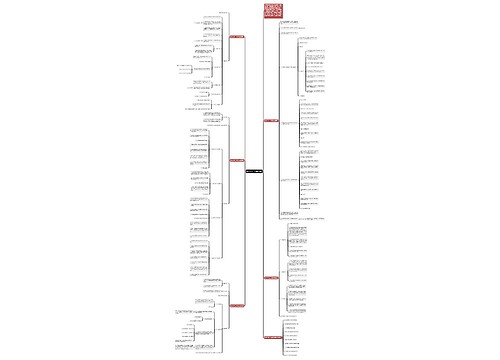
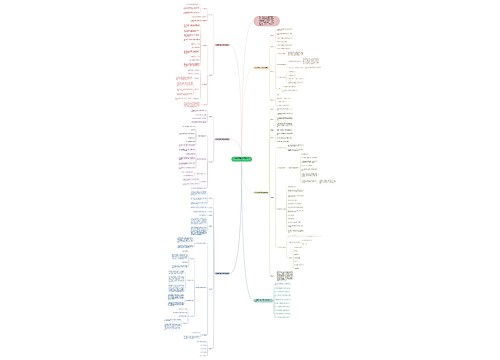
人教版高一年级数学知识点复习思维导图包含了以下几个知识点:函数的奇偶性、复合函数的有关问题、函数图像的对称性、函数的周期性、方程k=fx的值域范围、判断对应是否为映射和函数单调性的证明、反函数的求解和奇偶性的判断。其中函数的奇偶性包含到判断函数是否为奇偶函数、如何判断函数的奇偶形式和如何判断函数的单调性,复合函数的有关问题包含定义域的求法和单调性的判断,函数图像的对称性则需要证明函数图像的对称性和曲线的对称性,函数的周期性包含了不同类型的周期函数的定义和判定方法,方程k=fx的值域范围需要掌握根据定义判断值域的范围,并掌握相关的定理,判断对应是否为映射需要注意A中元素都有象、B中元素不一定都有原象和A中不同元素在B中可以有相同的象,还需要熟练地掌握函数单调性证明、反函数的求解和奇偶性的判断。
思维导图大纲
相关思维导图模版
人教版高一数学下册教学计划思维导图
 暖橙
暖橙树图思维导图提供《人教版高一数学下册教学计划》在线思维导图免费制作,点击“编辑”按钮,可对《人教版高一数学下册教学计划》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:b5f9ca88dec986b7f2676cec31783ce4
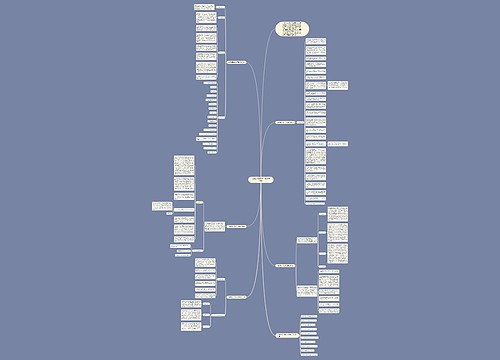
高一年级数学备课组教育教学计划思维导图
 没说出口的安慰
没说出口的安慰树图思维导图提供《高一年级数学备课组教育教学计划》在线思维导图免费制作,点击“编辑”按钮,可对《高一年级数学备课组教育教学计划》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:5501b48e3f8dd27ea1a453bf3b3c5ef0