八年级数学知识点总结北师大版思维导图
眼眶很热
2022-12-21

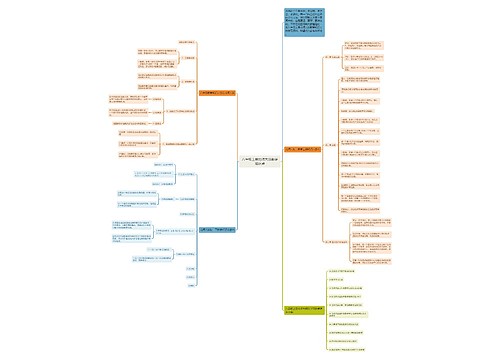
八年级数学知识点总结北师大版思维导图包含函数相关概念、数据的收集、整理与描述和四边形,在函数中,需要了解变量与常量的概念,掌握函数解析式、自变量取值范围,并学会用解析法、列表法、图像法三种方式表示函数关系,在数据收集整理与描述中,需要了解调查和抽样调查的区别,掌握样本容量、频数和频率。并了解如何分组和计算组距,在四边形中,需要了解平行四边形的定义、性质和判定方式,和矩形的定义、性质和判定定理。
思维导图大纲
相关思维导图模版
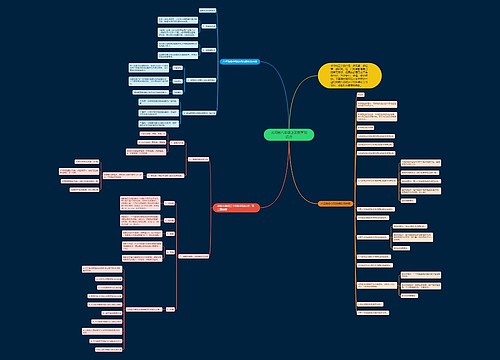
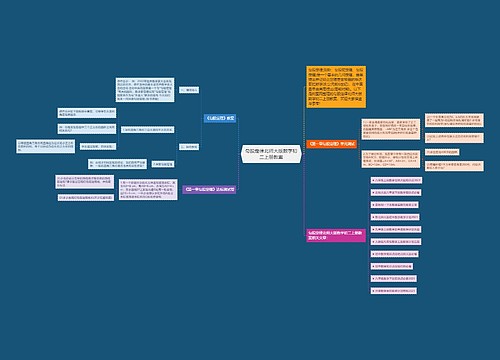
北师大版八年级数学上册知识点思维导图
 时光静好
时光静好树图思维导图提供《北师大版八年级数学上册知识点》在线思维导图免费制作,点击“编辑”按钮,可对《北师大版八年级数学上册知识点》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6ef2d0782b6685e4d8383e0e3bd4aae1
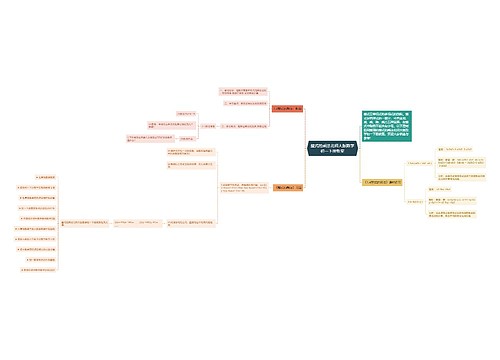
八年级上册北师大版数学知识点思维导图
 深知他心
深知他心树图思维导图提供《八年级上册北师大版数学知识点》在线思维导图免费制作,点击“编辑”按钮,可对《八年级上册北师大版数学知识点》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:7479aff88929ff5e2348e5c76338b86f