对于三年级学生寒假数学辅导之应用题的注意事项思维导图

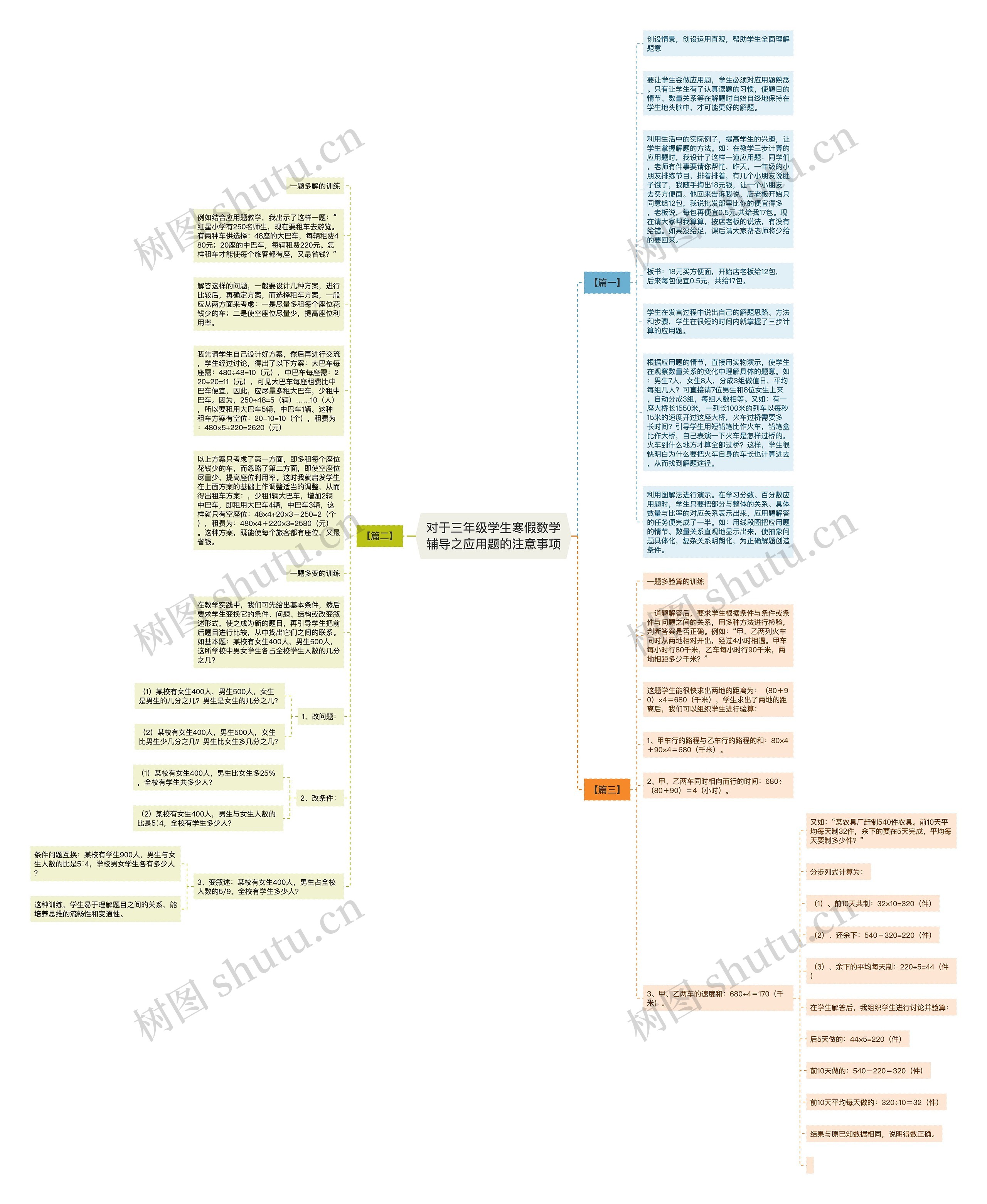
对于三年级学生寒假数学辅导之应用题的注意事项思维导图包含以下知识点：创设生动的情景，运用直观示例帮助学生理解题意。利用“一题多解”的方法，鼓励学生自己尝试解题，并进行交流，提高学生的解题能力，对于分数、百分数应用题，可以利用图解法进行演示，使学生直观地理解题目的情节和数量关系。通过实物演示，让学生通过观察数量关系的变化来更好的理解题目，一定要让学生养成认真读题的习惯，使题目的情节、数量关系在解题时能够自始至终地保持在学生的脑海中，才可能更好的解决问题。