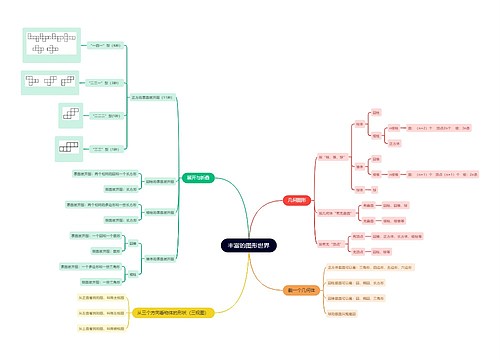
六年级数学小论文五篇思维导图
清泪尽
2022-12-21
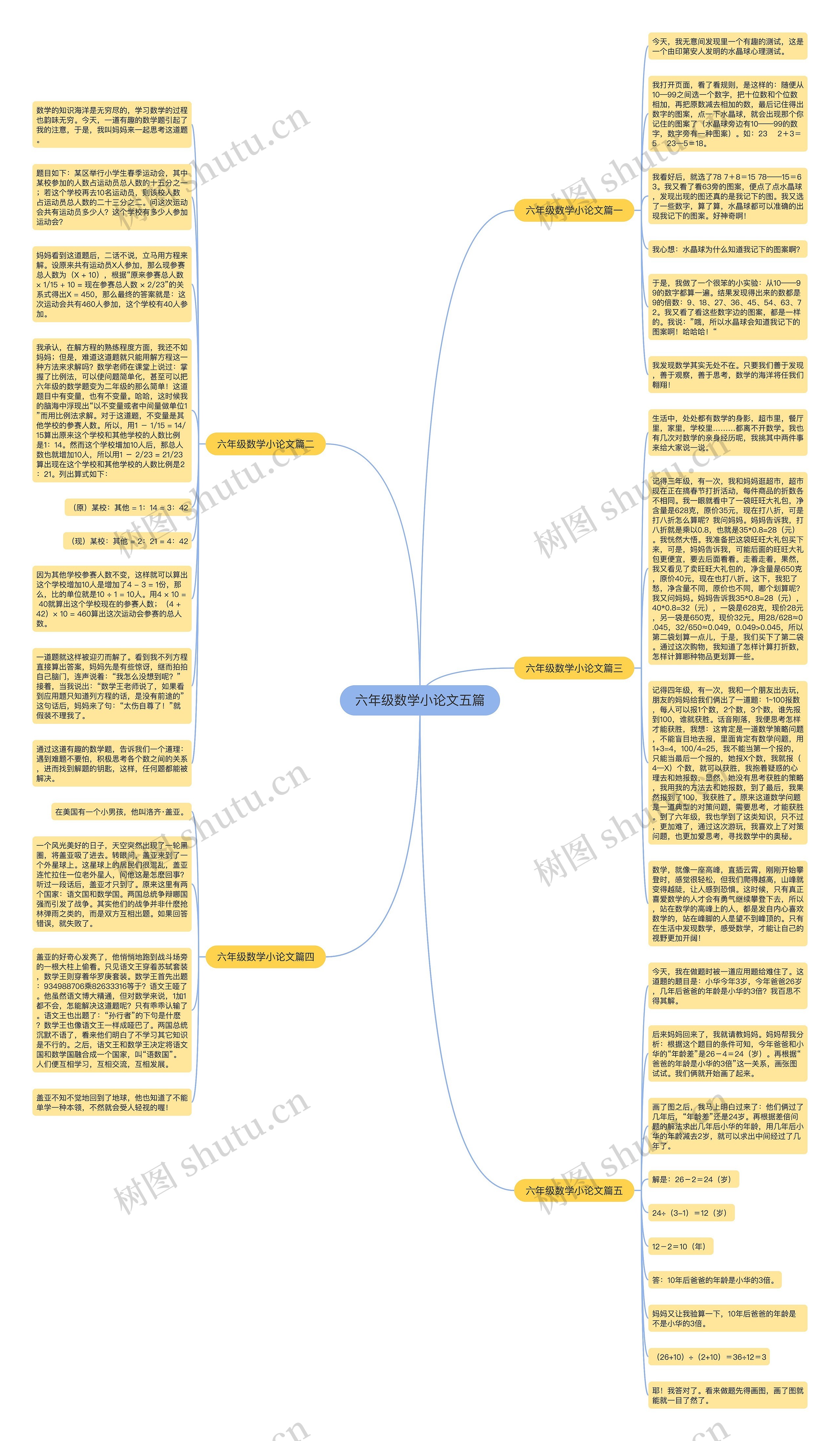
六年级数学小论文五篇思维导图,其中第一篇思维导图讲述了通过一道数学测试,发现水晶球心理测试会自动计算出结果,结果为9的倍数,而对应的图案都一样,认识到数学的无处不在,第二篇思维导图讲述了一道通过解方程来求解的问题,但提出了另一种思路,即通过比例法,以不变量或中间量做单位1来简单化问题,展示了数学的多样性。
思维导图大纲
相关思维导图模版
数学小学六年级教学总结怎么写思维导图
 堕落时代
堕落时代树图思维导图提供《数学小学六年级教学总结怎么写》在线思维导图免费制作,点击“编辑”按钮,可对《数学小学六年级教学总结怎么写》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:02815c0c8b7bb7f58df394352074a545
关于数学六年级教学总结思维导图
 我没你想的那样坚强
我没你想的那样坚强树图思维导图提供《关于数学六年级教学总结》在线思维导图免费制作,点击“编辑”按钮,可对《关于数学六年级教学总结》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:b1027e1ce636f4fc84a95253e2f8ba88