考研数学36个重要题型知识点树形图思维导图

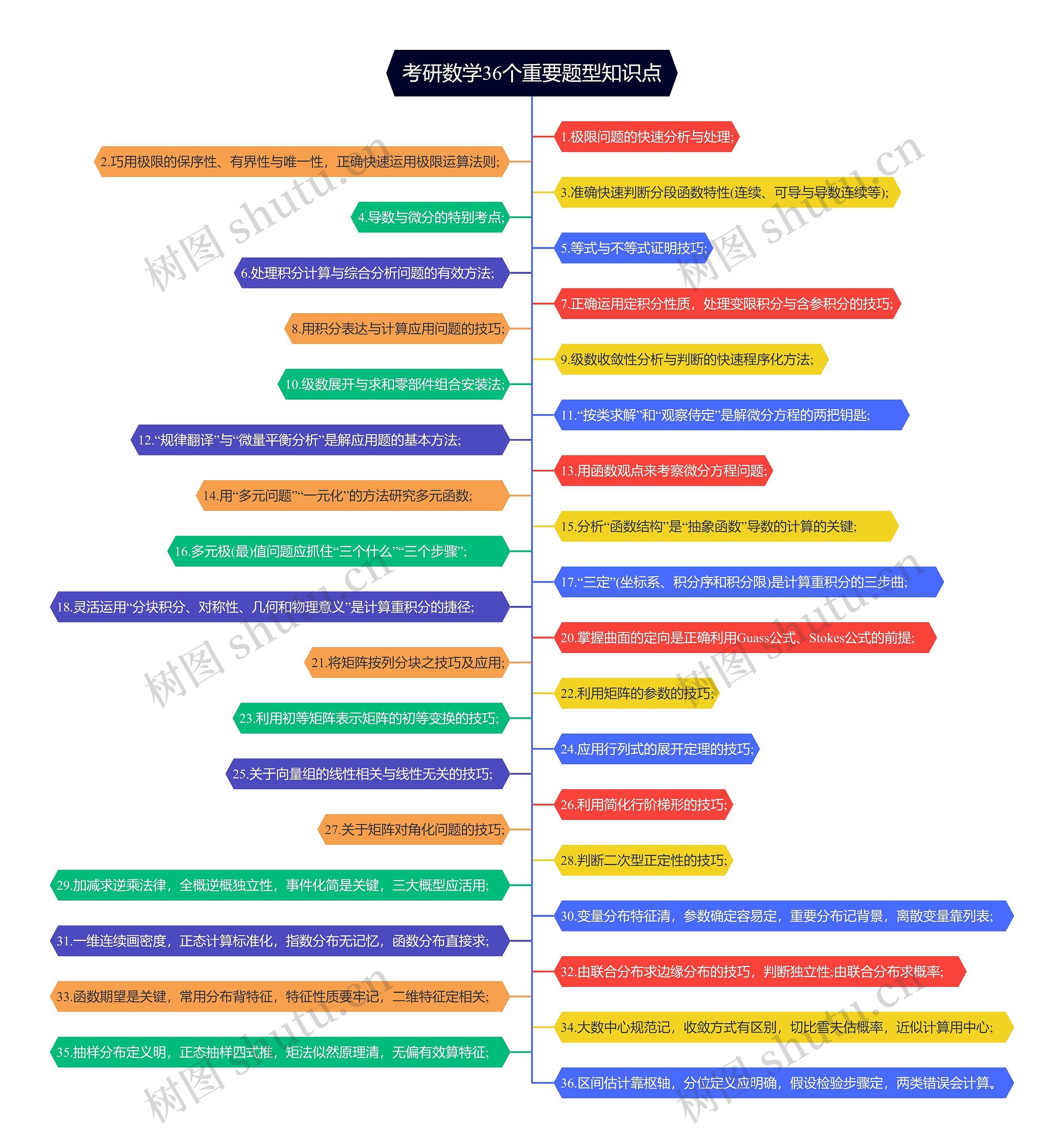
考研数学36个重要题型知识点树形图思维导图，涵盖了极限、分段函数、微积分、级数、微分方程、多元函数、重积分、曲线积分、矩阵、概率统计的内容。要掌握极限问题的快速分析处理、正确灵活运用极限运算法则和分段函数特性判断，要注意微分方程和应用题的解法，和函数观点来考察微分方程问题，在统计中，要清楚分布的特征和性质，特别要熟练掌握函数期望和联合分布求概率的方法，还需掌握如何判断二次型正定性，和假设检验的步骤和计算两类错误的方法。