2017高考数学函数与导数知识点汇总思维导图

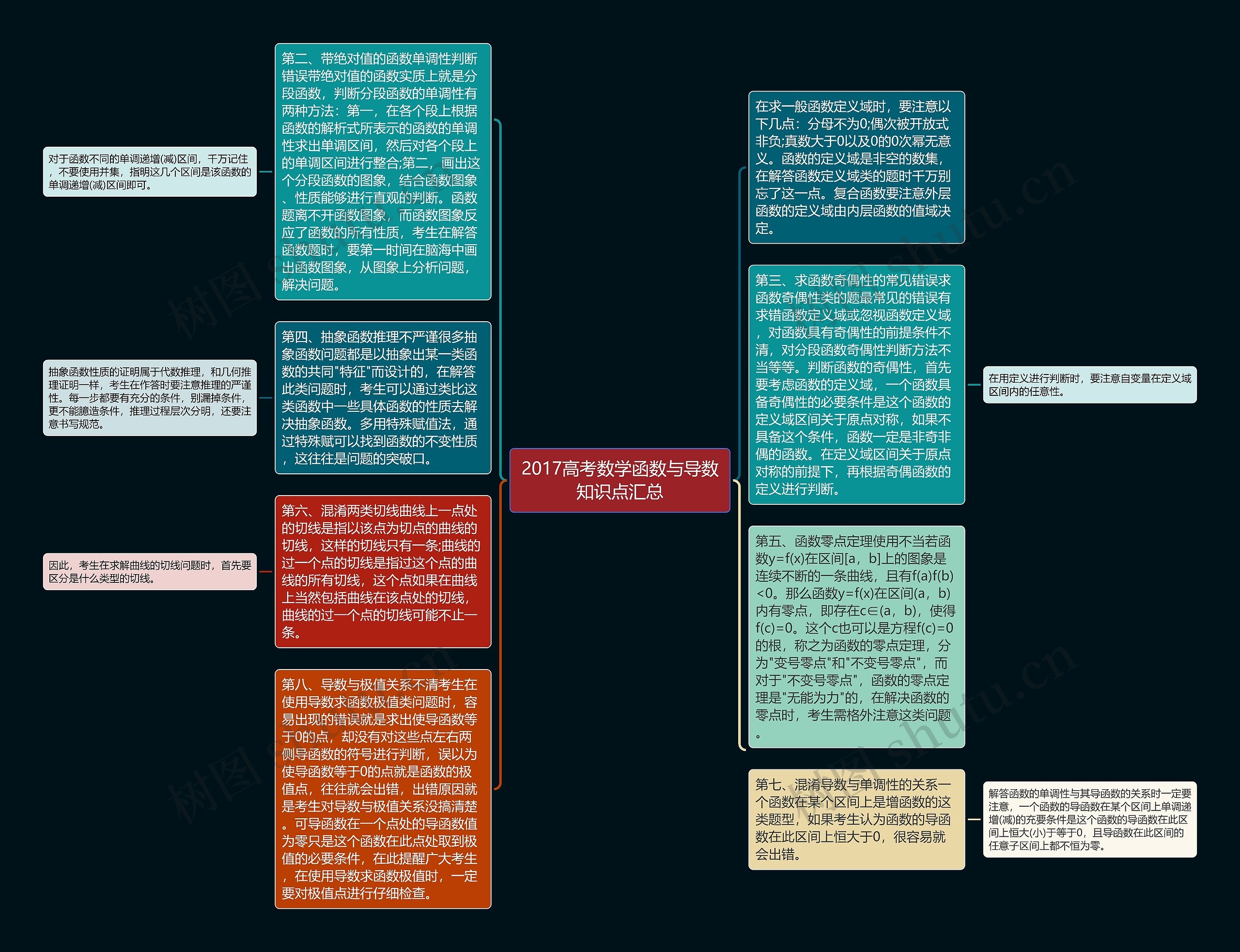
2017高考数学函数与导数知识点汇总思维导图的知识点是这样的：在求一般函数的定义域时，要注意几个要点：分母不能为0，偶次开方的非负数，正数大于0，而0的0次幂没有意义。要记住函数的定义域是一个非空的数集，解决和定义函数的相关问题时千万别忘记这一点，当包含到复合函数时，要注意外层函数的定义域是由内层函数的值域决定的。

判断带绝对值的函数的单调性时容易出错。这类函数实质上是分段函数，判断分段函数的单调性有两种方法：第一种是在各段上根据函数的解析式所表示的函数的单调性分析出单调区间，整合各个段上的单调区间，第二种是画出这个分段函数的图像，通过观察图像和性质来进行直观判断。函数题离不开函数图像，而函数图像反映了函数的所有性质，考生在解答函数题时，要第一时间在脑海中画出函数图像，通过观察图像分析和解决问题。

对于函数不同的单调递增（递减）区间，要记住不要使用并集，只需要指明这几个区间是该函数的单调递增（递减）区间。

第三，求函数奇偶性常常犯错。在求函数奇偶性的问题中，最常见的错误有求错函数的定义域或忽视函数的定义域，对函数具有奇偶性的前提条件不清楚，对分段函数奇偶性判断方法不当等，判断函数的奇偶性，首先要考虑函数的定义域，一个函数奇偶性的必要条件是这个函数的定义域区间关于原点对称，如果不具备这个条件，那么函数一定是非奇非偶的函数。在定义域区间关于原点对称的前提下，根据奇偶函数的定义进行判断时，要注意自变量在定义域区间内的任意性。

第四，抽象函数推理不严谨。很多抽象函数问题都是基于共同的“特征”而设计的，解决这类问题时，可以通过类比这类函数中的一些具体函数的性质来解决抽象函数的问题，多用特殊赋值法，通过特殊的赋值，可以找到函数的不变性质，这往往是解决问题的关键。

对于抽象函数性质的证明，属于代数推理，和几何推理证明一样，在作答时要注意推理的严谨性。每一步都要有充分的条件，别漏掉条件，更不能凭空臆造条件，推理过程要层次分明，同时要注意书写规范。

函数零点定理的使用有时容易出错。如果函数y=f(x)在区间[a，b]上的图像是连续不断的曲线，且有f(a)f(b)<0，那么函数y=f(x)在区间(a，b)内有零点，也就是说存在c∈(a，b)，使得f(c)=0。这个c也可以是方程f(c)=0的根，称为函数的零点定理，函数的零点定理分为“变号零点”和“不变号零点”，对于“不变号零点”，函数的零点定理无法解决。在解决函数的零点时，考生需要特别注意这类问题。

以上就是2017高考数学函数与导数知识点汇总思维导图的知识点总结，希望可以帮到你，如果还有其他问题，请随时告诉我。