2018高考数学答题方法:立体几何解题技巧思维导图
堕落时代
2023-04-20
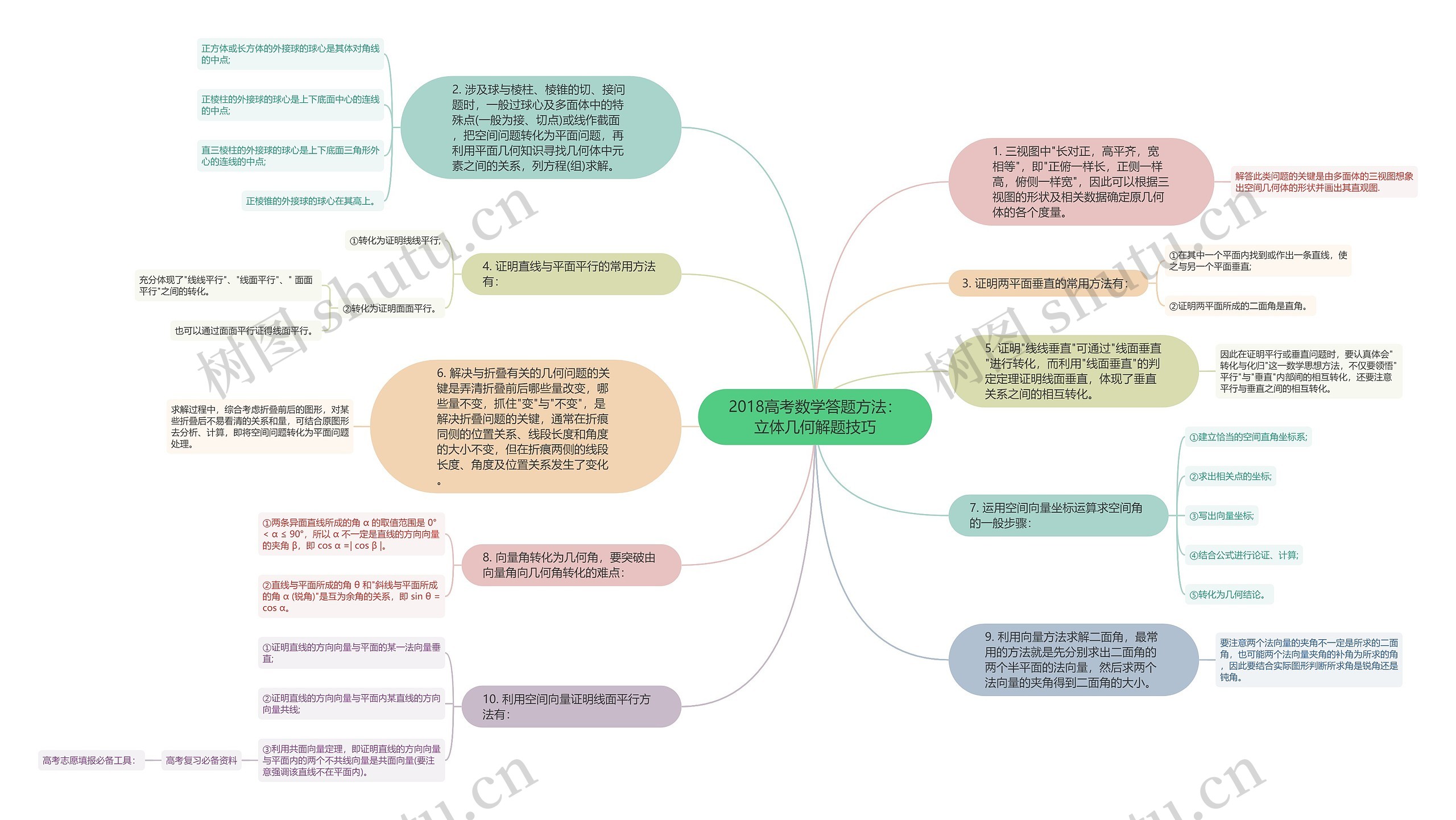
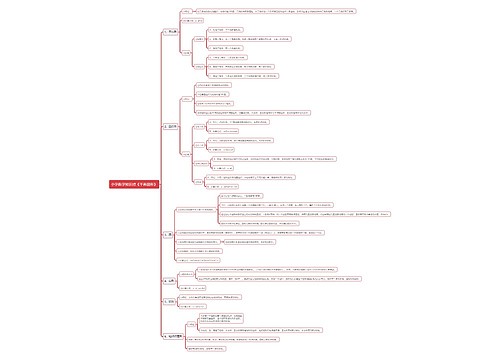
2018年高考数学考试有关立体几何解题的技巧思维导图内容包含以下几点:1.在三视图中,长对正、高平齐、宽相等的规律,利用三视图的形状和相关数据确定几何体的度量。
2.当包含球和棱柱、棱锥的切和接问题时,可以通过截面求解,将空间问题转化为平面问题。正方体或长方体的外接球的球心是体对角线的中点。
3.证明两平面垂直的常用方法有:在一个平面内找到或作出一条与另一个平面垂直的直线,或证明两平面所成的二面角是直角。
4.证明直线与平面平行的常用方法有:转化为证明线线平行或面面平行。可以通过面面平行证得线面平行。
5.证明线线垂直可以通过线面垂直进行转化,利用线面垂直的判定定理进行证明。体现了垂直关系之间的相互转化。
6.解决折叠问题的关键是确定哪些量变化,哪些量不变。抓住变与不变是解决折叠问题的关键,通常折痕同侧的位置关系、线段长度和角度大小不变,而在折痕两侧的线段长度、角度和位置关系会发生变化。
7.运用空间向量坐标运算求解空间角的一般步骤包含:建立适当的空间直角坐标系、求出相关点的坐标、写出向量坐标、结合公式进行论证和计算,最后转化为几何结论。
以上是2018高考数学答题方法:立体几何解题技巧思维导图中的知识点,通过运用这些知识点,可以更好的应对高考数学立体几何题目。
思维导图大纲
相关思维导图模版
2018高考数学答题方法:高考数学冲刺注意要点思维导图
 清风和酒
清风和酒树图思维导图提供《2018高考数学答题方法:高考数学冲刺注意要点》在线思维导图免费制作,点击“编辑”按钮,可对《2018高考数学答题方法:高考数学冲刺注意要点》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6d77d183be5d41546d34a0a97408b281
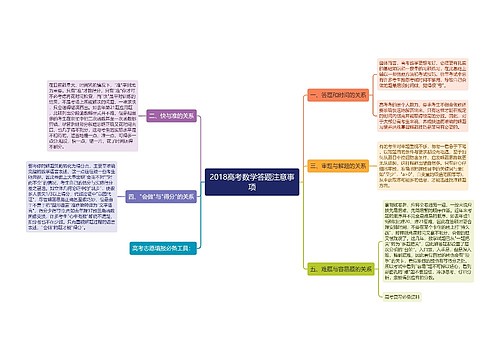
2018高考数学答题注意事项思维导图
 旧街悲巷
旧街悲巷树图思维导图提供《2018高考数学答题注意事项》在线思维导图免费制作,点击“编辑”按钮,可对《2018高考数学答题注意事项》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:de846231007c96abc42fba7773c31716