高考数学知识点总结：平面向量公式思维导图

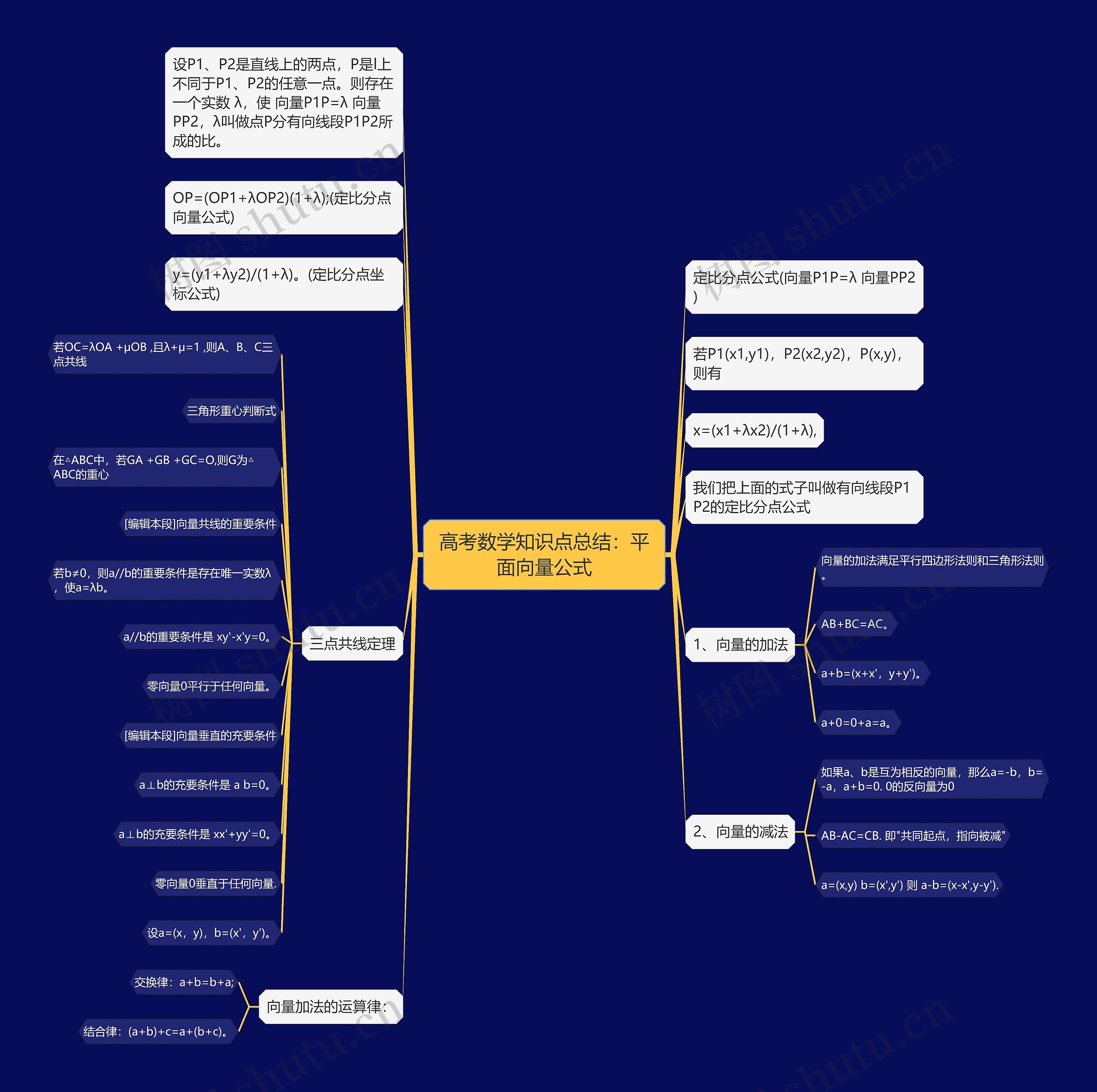
高考数学知识点解析：平面向量公式，树图网高考频道收录整理，希望对高考学子备考有所帮助。

树图思维导图提供《高考数学知识点总结：平面向量公式》在线思维导图免费制作，点击“编辑”按钮，可对《高考数学知识点总结：平面向量公式》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：3fcfebb3edcf343a60e83bf77c5fcfe5