高二数学备考："充要条件"具体概念思维导图

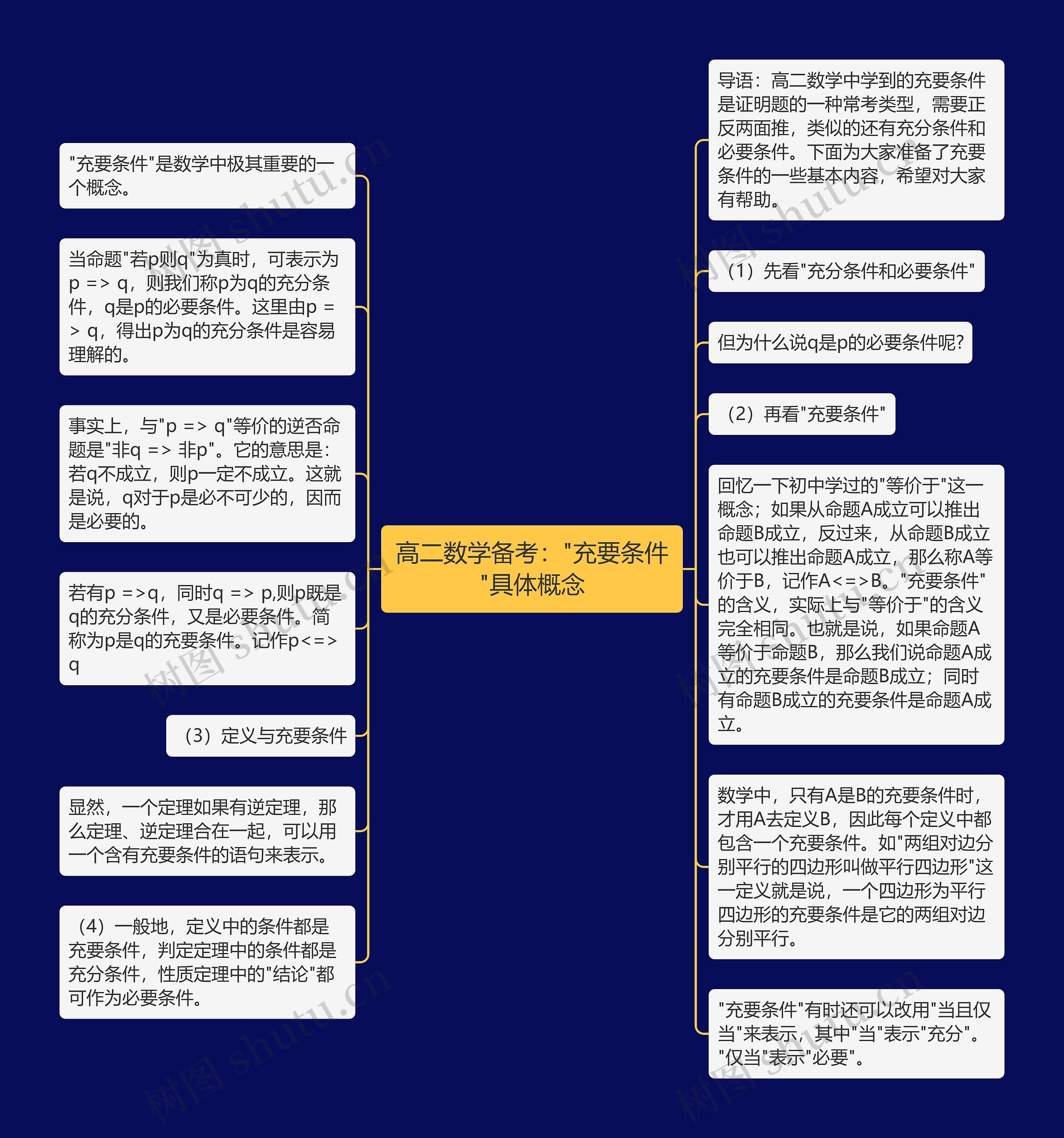
高二数学备考："充要条件"具体概念思维导图是为了帮助大家梳理充要条件的知识点而设计的。在高二数学中，充要条件是证明题中常见的一种类型，需要通过正反两个方向进行推导，还包含充分条件和必要条件。首先我们来看充分条件和必要条件的概念，当命题"若p则q"为真时，可以将其表示为p=>q，这时我们称p为q的充分条件，而q是p的必要条件。为什么q是p的必要条件呢？实际上，可以通过逆否命题"非q=>非p"来理解，如果q不成立，则p一定不成立，所以q对于p是必不可少的，也就是必要条件。接下来我们来看充要条件的概念，如果有p=>q同时q=>p/，那么p既是q的充分条件，又是必要条件，简称为p是q的充要条件，记作p<=>q。可以回忆一下初中学过的"等价于"的概念，如果命题A成立可以推出命题B成立，反过来，从命题B成立也可以推出命题A成立，那么称A等价于B，记作A<=>B。实际上，"充要条件"的含义与"等价于"的含义完全相同，也就是说，如果命题A等价于命题B，那么命题A成立的充要条件就是命题B成立，同时命题B成立的充要条件就是命题A成立。在数学中，只有A是B的充要条件时才可以用A去定义B，因此每个定义中都包含一个充要条件。平行四边形的定义就是说，一个四边形为平行四边形的充要条件是他的两组对边分别平行，一个定理如果存在逆定理，那么定理和逆定理可以用一个含有充要条件的语句来表示。有时，我们也可以将"充要条件"替换为"当且仅当"，其中"当"表示充分条件，而"仅当"表示必要条件。总的来说，定义中的条件一般都是充要条件，判定定理中的条件一般是充分条件，而性质定理中的"结论"则可以作为必要条件，希望通过本导图对充要条件的概念有更清晰的了解，对高二数学备考有所帮助。