高二数学备考：数学解析几何中求参数取值范围的方法一思维导图

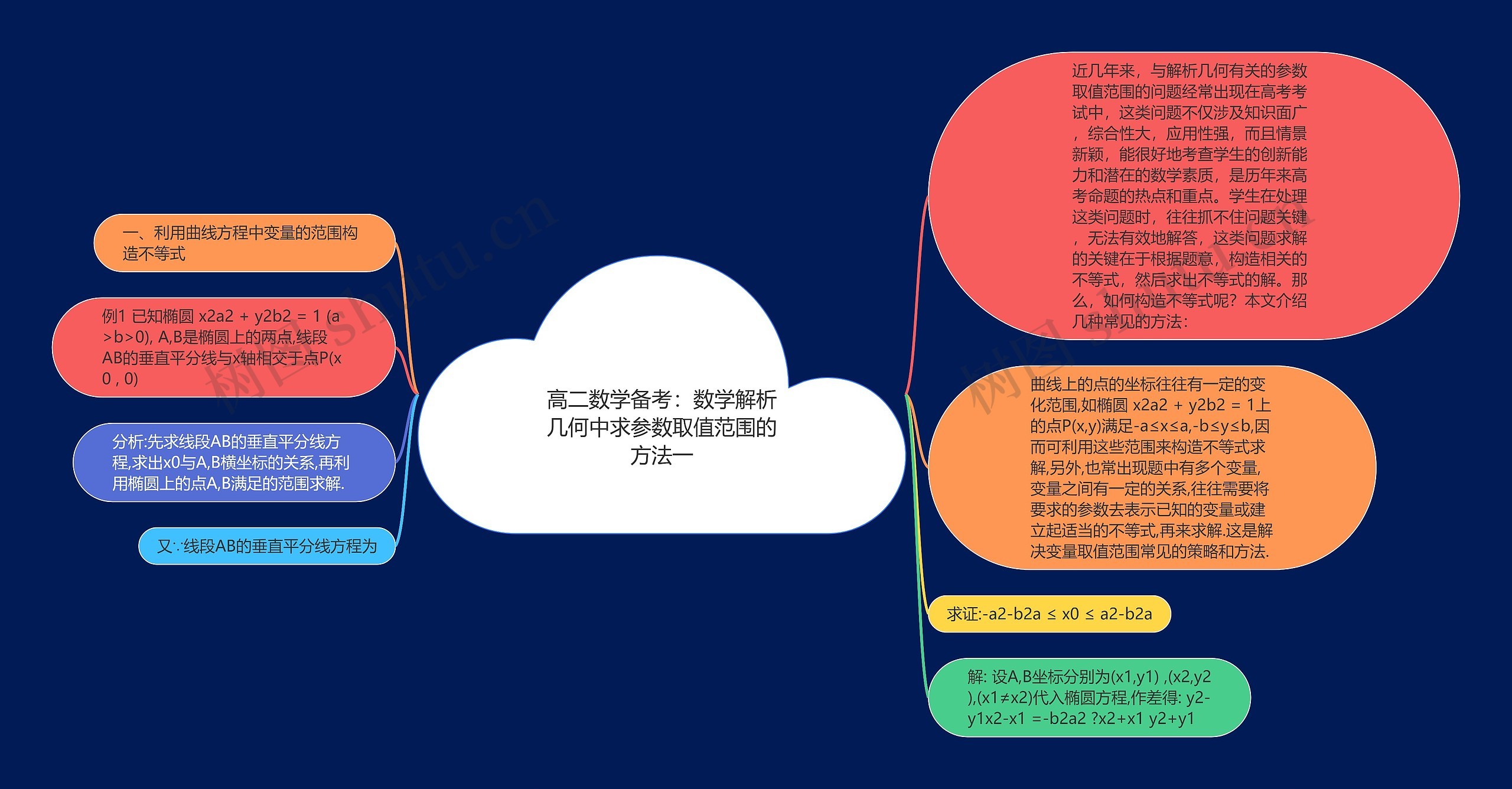
高二数学备考：数学解析几何中求参数取值范围的方法一思维导图，近几年来，高考中经常包含解析几何的参数取值范围问题。这类问题不仅知识面广、综合性强，而且具有很强的应用性和创新性，能够考察学生的数学素质和创新能力，是命题的热点和重点，处理这类问题时，学生常常不能抓住问题的关键，无法有效地解答。而这类问题的求解关键在于根据题意，构造相关的不等式，求解这些不等式，如何构造不等式呢？本模板将介绍几种常见的方法。

可以利用曲线方程中变量的范围构造不等式。曲线上的点的坐标往往有一定的变化范围，椭圆x22+y22=1/上的点P(x,y)满足-a≤x≤a，-b≤y≤b，/可以利用这些范围来构造不等式并求解。题目中常常出现多个变量，变量之间存在一定的关系，这时常常需要将要求的参数表示为已知的变量或建立适当的不等式，进行求解，这是解决变量取值范围问题的常见策略和方法。

以一个例子来说明这种方法的应用。已知椭圆x22+y22=1/(a>b>0)，A、B是椭圆上的两个点，线段AB的垂直平分线与x轴相交于点P(x0,0)。要求证明：-a2-b2a≤x0≤a2-b2a。

分析/：首先求解线段AB的垂直平分线方程，求出x0与A、B横坐标的关系，利用椭圆上的点A、B满足的范围进行求解。

解答：设点A、B的坐标分别为(x1,y1)、(x2,y2)，代入椭圆方程，并作差，得到y2-y12-x1=-b22*(x2+x1)/(y2+y1)。

由于线段AB的垂直平分线方程与x轴相交于点P(x0,0)，所以y2+y1=0，代入上式可得x0=-b22*(x2+x1)。

又因为椭圆上的点A、B满足-a≤x≤a，即-a≤x1,x2≤/a，代入x0的表达式中，得到-b22*(2a)≤x0≤-b22*(-2a)，即-a2-b2a≤x0≤a2-b2a。

通过以上步骤，可以证明参数x0的取值范围为-a2-b2a≤x0≤a2-b2a/。