高二数学备考：判断充分与必要条件的常用方法思维导图

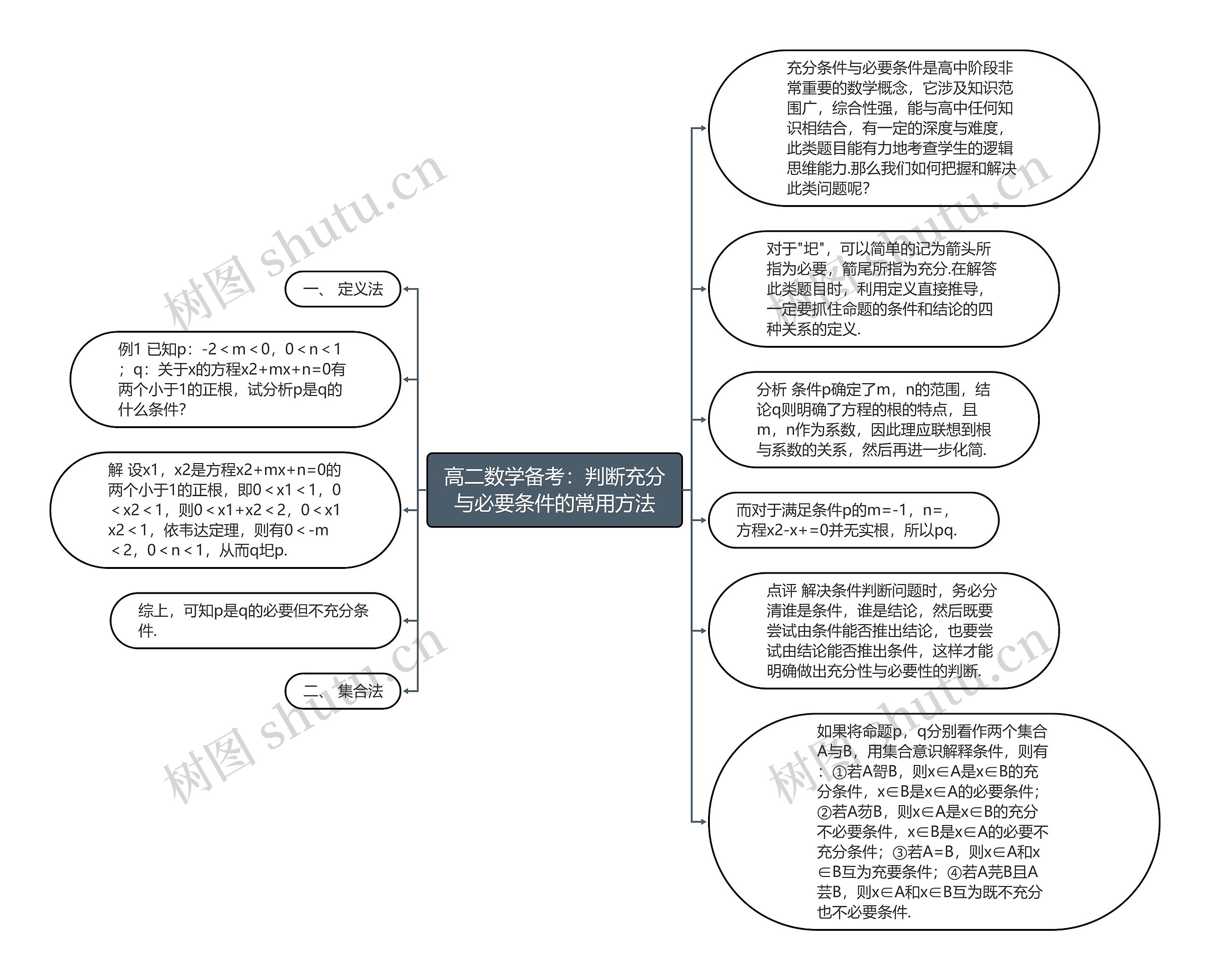
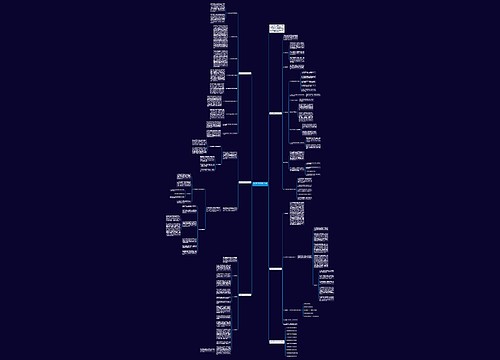
高二数学备考：判断充分与必要条件的常用方法思维导图模板大纲，判断充分条件与必要条件是高中阶段非常重要的数学概念。他涉及的知识范围广泛，综合性强，能与高中任何知识相结合，有一定的深度和难度，解决此类问题需要我们掌握以下知识点。

一、定义法

在解答此类题目时，可以利用定义直接推导。需要抓住命题的条件和结论的四种关系的定义，已知条件p确定了m，n的范围，结论q明确了方程的根的特点，可以联想到根与系数的关系，进一步化简。通过推导可以判断p是否是q的条件。

二、集合法

将命题p和q分别看作两个集合A和B，用集合意识解释条件。根据集合的关系，可以得出以下结论：

1.若A包含于B，则x∈A是x∈B的充分条件，x∈B是x∈A的必要条件。

2.若A不完全包含于B，则x∈A是x∈B的充分不必要条件，x∈B是x∈A的必要不充分条件。

3.若A与B相等，则x∈A和x∈B互为充要条件。

4.若A与B既不完全包含于对方，也不相等，则x∈A和x∈B互为既不充分也不必要条件。

掌握上述方法，能够清晰地判断条件和结论之间的关系，解决判断充分与必要条件的问题，这对于培养学生的逻辑思维能力具有重要意义，在高二数学备考中，需要熟练掌握并灵活运用这些方法。