高二数学备考:"三角函数"公式大全2思维导图
青烟
2023-04-20

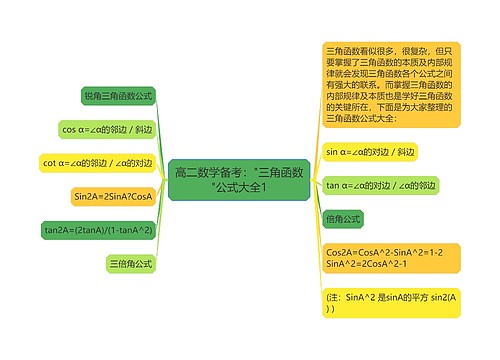
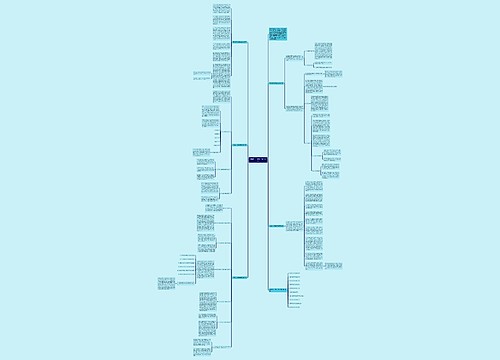
高二数学备考中的一个知识点是三角函数公式,包含了一些推导公式和半角公式。推导公式涵盖了tanα+cotα=22α、tanα-cotα=-2cot2α、1+cos2α=2cos^2α、1-cos2α=2sin^2α、1+sinα=(sinα/2+cosα/2)^2、cos3a=4cos3a-3cosa、sin3a=3sina-4sin3a等公式。半角公式则包含了tan(A/2)=(1-cosA)/sinA和cot(A/2)=sinA/(1-cosA),还有三角和公式sin(α+β+γ)、cos(α+β+γ)和tan(α+β+γ)的计算公式,通过掌握这些重要的三角函数公式,能够有效地解决数学备考中的问题。
思维导图大纲
相关思维导图模版
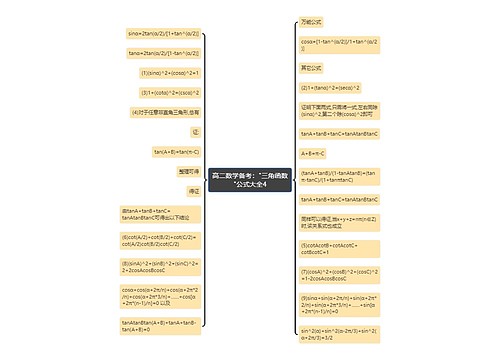
高二数学备考:"三角函数"公式大全4思维导图
 谁相伴
谁相伴树图思维导图提供《高二数学备考:"三角函数"公式大全4》在线思维导图免费制作,点击“编辑”按钮,可对《高二数学备考:"三角函数"公式大全4》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:260d7933240c62def7c93b45aeceb87d
高二数学备考:"三角函数"公式大全3思维导图
 眼眶很热
眼眶很热树图思维导图提供《高二数学备考:"三角函数"公式大全3》在线思维导图免费制作,点击“编辑”按钮,可对《高二数学备考:"三角函数"公式大全3》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:80d1645d247a23fb887e2503fe470eda