高二数学复习方法：数学三角函数知识点思维导图

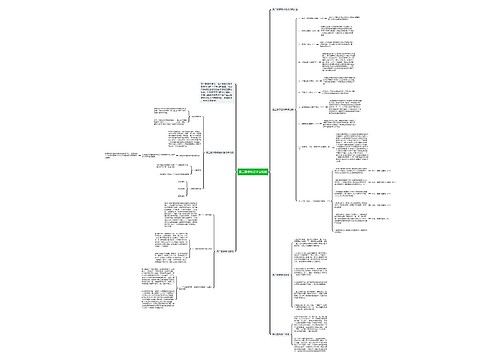
高二数学复习方法：数学三角函数知识点思维导图，在高二数学复习过程中，数学三角函数是一个重要的内容。在这个知识点中，需要掌握锐角三角函数的定义，如正弦、余弦、正切、余切、正割和余割的含义与计算方法，我们还需要了解互余角的三角函数之间的关系，和平方关系、积的关系、倒数关系。

在锐角三角函数的定义中，知道正弦(sin)等于对边a除以斜边c，余弦(cos)等于邻边b除以斜边c，正切(tan)等于对边a除以邻边b，余切(cot)等于邻边b除以对边a，正割(sec)等于斜边c除以邻边b，余割(csc)等于斜边c除以对边a。

而互余角的三角函数间的关系即，在角A和角B为互余角时，有sin(90°-A)=cosA,cos(90°-A)=sinA,tan(90°-A)=cotA,cot(90°-A)=tanA。

平方关系指的是sin^2(α)+cos^2(α)=1,tan^2(α)+1=sec^2(α),cot^2(α)+1=csc^2(α)。

积的关系有sinα=tanα·cosα,cosα=cotα·sinα,tanα=sinα·secα,cotα=cosα·cscα,secα=tanα·cscα,cscα=secα·cotα。

还有一些三角和的三角函数公式，如sin(A+B)=sinAcosB+cosAsinB，cos(A+B)=cosAcosB-sinAsinB等，还有辅助角公式、倍角公式、三倍角公式、半角公式等，这些公式都非常重要。

还有一些其他的关系，如tanA+cotA=22A,sinα.sin(α+2π)+sinα.sin(α+2π*2)+sinα.sin(α+2π*3)+……+sinα.sin[α+2π*(n-1)]=0等。

可以利用一个六边形的记忆模型，上弦表示sin，中切表示tan，下割表示cot，左正表示cos，右余表示csc，中间的1表示sec，帮助我们记忆六角函数之间的关系。

通过掌握这些重要的内容，可以更好的复习数学三角函数，在考试中取得好成绩。