高一数学教案:交集与并集(3)思维导图
定格苍凉
2023-04-20

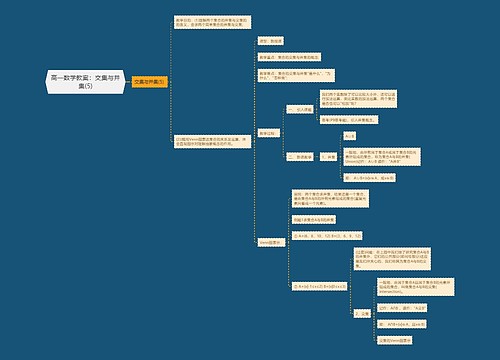
教案通常又叫教学设计,包括教材简析和学生分析、教学目的、重难点、教学准备、教学过程及练习设计等。树图网为大家整理了《高一数学教案:交集与并集(3)》,供大家参考。
树图思维导图提供《高一数学教案:交集与并集(3)》在线思维导图免费制作,点击“编辑”按钮,可对《高一数学教案:交集与并集(3)》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:a7a6e9e02606592756d57772b1736b93
思维导图大纲
相关思维导图模版
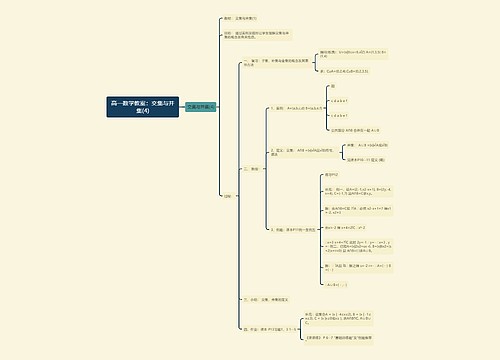
高一数学教案:交集与并集(4)思维导图
 女痞
女痞树图思维导图提供《高一数学教案:交集与并集(4)》在线思维导图免费制作,点击“编辑”按钮,可对《高一数学教案:交集与并集(4)》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:77f643bd19d840fb3c5cf9c20b6285da
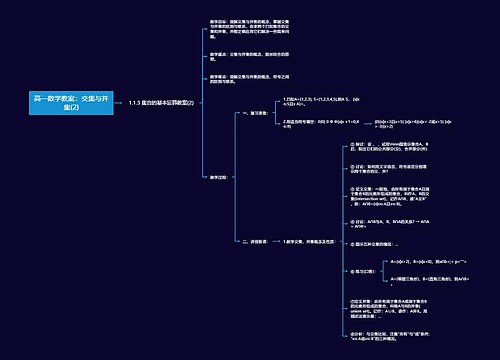
高一数学教案:交集与并集(2)思维导图
 以为你会等我
以为你会等我树图思维导图提供《高一数学教案:交集与并集(2)》在线思维导图免费制作,点击“编辑”按钮,可对《高一数学教案:交集与并集(2)》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:7d4ac02dd508fa3d6ac55bb657f71899