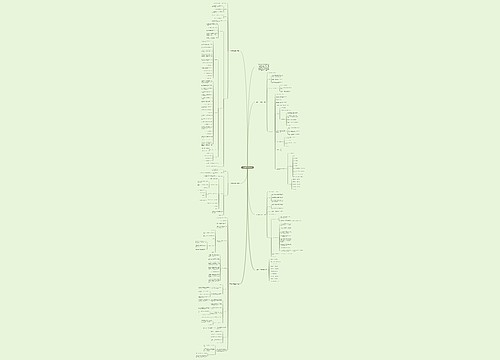
教师资格证数学常考知识点：一元一次方程思维导图

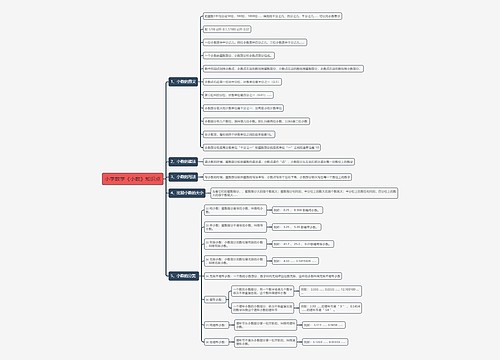
教师资格证数学常考知识点：一元一次方程思维导图，包含一元一次方程的概念、求根方法和应用，一元一次方程是指只有一个未知数且未知数的最高次数为1的等式，一般形式为ax+b=c，求解一元一次方程需要进行五步操作：去分母、去括号、移项、合并同类项、系数化为1。应用一元一次方程时，要注意找准等量关系，设定未知数，并将文字表达式转化为数学表达式列出方程并解方程，一元一次方程广泛应用于工程问题、行程问题、分配问题、盈亏问题、电话计费问题。