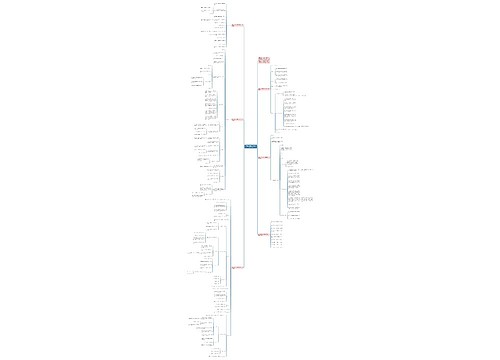
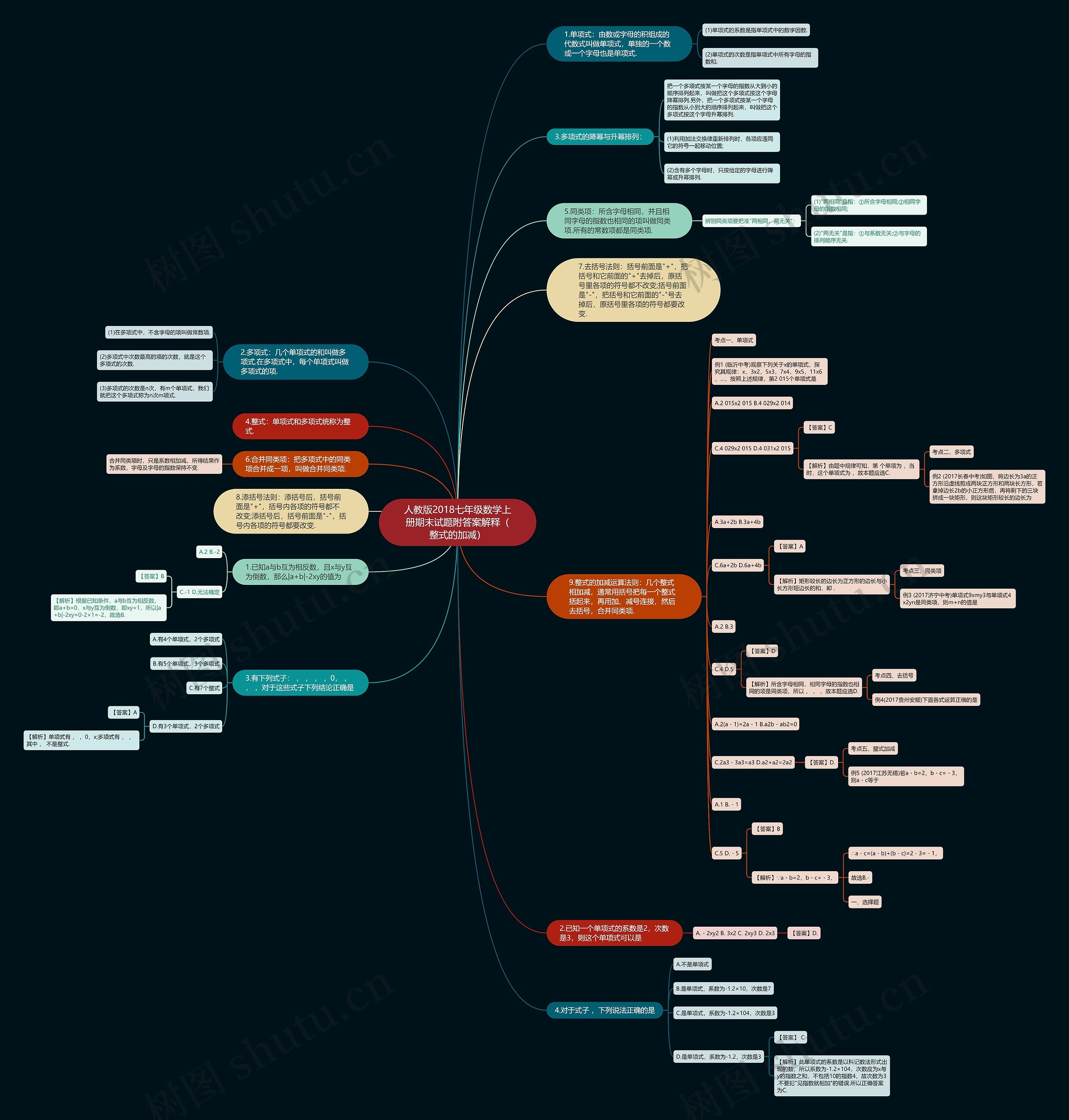
1.单项式:由数或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也是单项式.
2.多项式:几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.
(2)多项式中次数最高的项的次数,就是这个多项式的次数.
(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.
3.多项式的降幂与升幂排列:
把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.
(1)利用加法交换律重新排列时,各项应连同它的符号一起移动位置;
(2)含有多个字母时,只按给定的字母进行降幂或升幂排列.
5.同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.
辨别同类项要把准"两相同,两无关":
(1)"两相同"是指:①所含字母相同;②相同字母的指数相同;
(2)"两无关"是指:①与系数无关;②与字母的排列顺序无关.
6.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项.
合并同类项时,只是系数相加减,所得结果作为系数,字母及字母的指数保持不变.
7.去括号法则:括号前面是"+",把括号和它前面的"+"去掉后,原括号里各项的符号都不改变;括号前面是"-",把括号和它前面的"-"号去掉后,原括号里各项的符号都要改变.
8.添括号法则:添括号后,括号前面是"+",括号内各项的符号都不改变;添括号后,括号前面是"-",括号内各项的符号都要改变.
9.整式的加减运算法则:几个整式相加减,通常用括号把每一个整式括起来,再用加、减号连接,然后去括号,合并同类项.
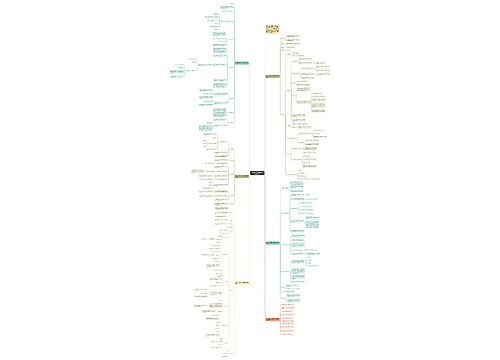
例1 (临沂中考)观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6,…,按照上述规律,第2 015个单项式是
A.2 015x2 015 B.4 029x2 014
C.4 029x2 015 D.4 031x2 015
【解析】由题中规律可知,第 个单项为 ,当 时,这个单项式为 ,故本题应选C.
例2 (2017长春中考)如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形,若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为
C.6a+2b D.6a+4b
【解析】矩形较长的边长为正方形的边长与小长方形短边长的和,即 .
例3 (2017济宁中考)单项式9xmy3与单项式4x2yn是同类项,则m+n的值是
C.4 D.5
【解析】所含字母相同,相同字母的指数也相同的项是同类项,所以 , , ,故本题应选D.
A.2(a﹣1)=2a﹣1 B.a2b﹣ab2=0
C.2a3﹣3a3=a3 D.a2+a2=2a2
【答案】D.
例5 (2017江苏无锡)若a﹣b=2,b﹣c=﹣3,则a﹣c等于
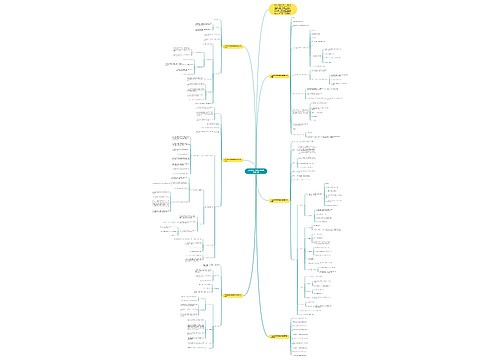
1.已知a与b互为相反数,且x与y互为倒数,那么|a+b|-2xy的值为
C.-1 D.无法确定
【解析】根据已知条件,a与b互为相反数,即a+b=0,x与y互为倒数,即xy=1,所以|a+b|-2xy=0-2×1=-2,故选B.
2.已知一个单项式的系数是2,次数是3,则这个单项式可以是
A.﹣2xy2 B. 3x2 C. 2xy3 D. 2x3
3.有下列式子: , , , ,0, , , ,对于这些式子下列结论正确是
D.有3个单项式,2个多项式
【解析】单项式有 , ,0,x;多项式有 , ,其中 , 不是整式.
4.对于式子 ,下列说法正确的是
D.是单项式,系数为-1.2,次数是3
【解析】此单项式的系数是以科记数法形式出现的数,所以系数为-1.2×104,次数应为x与y的指数之和,不包括10的指数4,故次数为3.不要犯"见指数就相加"的错误.所以正确答案为C.
 U633687664
U633687664
 U582679646
U582679646