初一数学基础知识2022思维导图
回憶褶皺
2023-04-11

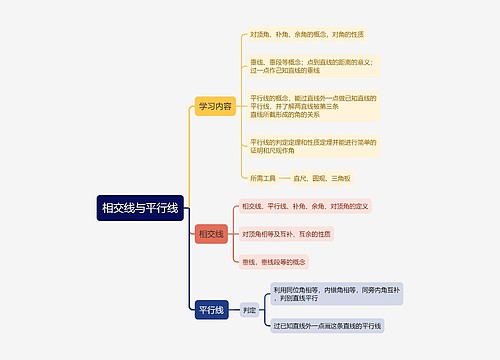
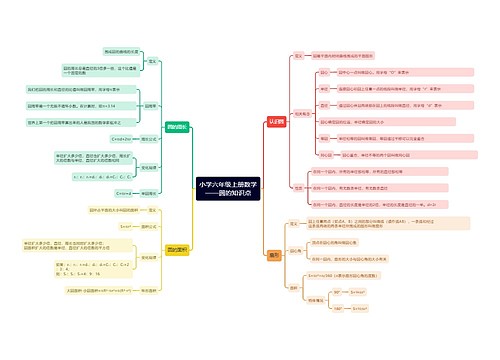
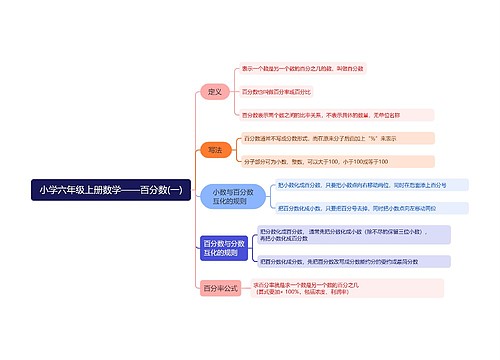
初一数学基础知识2022思维导图包含七年级数学知识点的总结,的知识点有三个:已知面积和底边长求高,求等边三角形的高,已知边长和角求高。对于已知面积和底边长求高,需要将面积和底边长代入公式A=1/2bh计算高,其中h等于面积除以底边长在乘以2。求等边三角形的高需要用勾股定理将直角边表示为a和b、斜边为c,对半切开,斜边c等于原始的边长,直角边a的长度就是边长的1/2,直角边b就是所求三角形的高。已知边长和角求高就需要确定已知的变量,使用海伦公式或面积公式求解,以上三个知识点是初一数学基础知识中必须掌握的。
思维导图大纲
相关思维导图模版
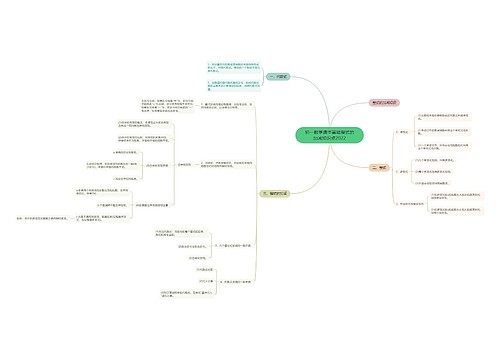
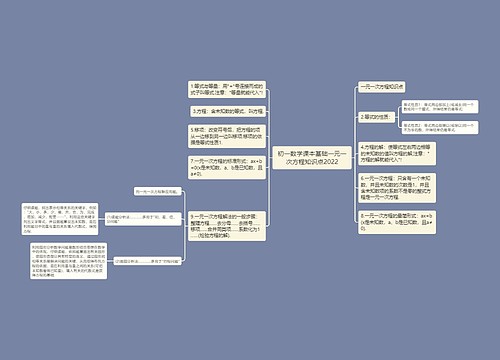
初一数学课本基础一元一次方程知识点2022思维导图
 我没你想的那样坚强
我没你想的那样坚强树图思维导图提供《初一数学课本基础一元一次方程知识点2022》在线思维导图免费制作,点击“编辑”按钮,可对《初一数学课本基础一元一次方程知识点2022》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:b6ef0712da70394c56fa91344e2bc289
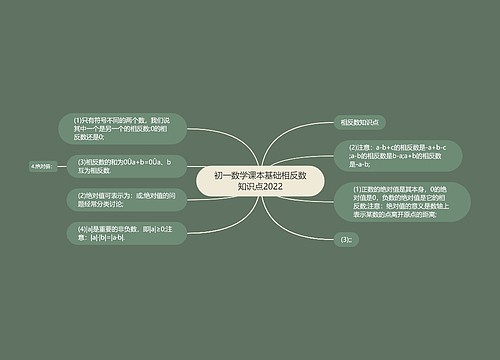
初一数学课本基础相反数知识点2022思维导图
 心不动则不痛
心不动则不痛树图思维导图提供《初一数学课本基础相反数知识点2022》在线思维导图免费制作,点击“编辑”按钮,可对《初一数学课本基础相反数知识点2022》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:0ed56bba8d18dede12f0a02436212ccc