九年级数学教师个人教学反思模板思维导图

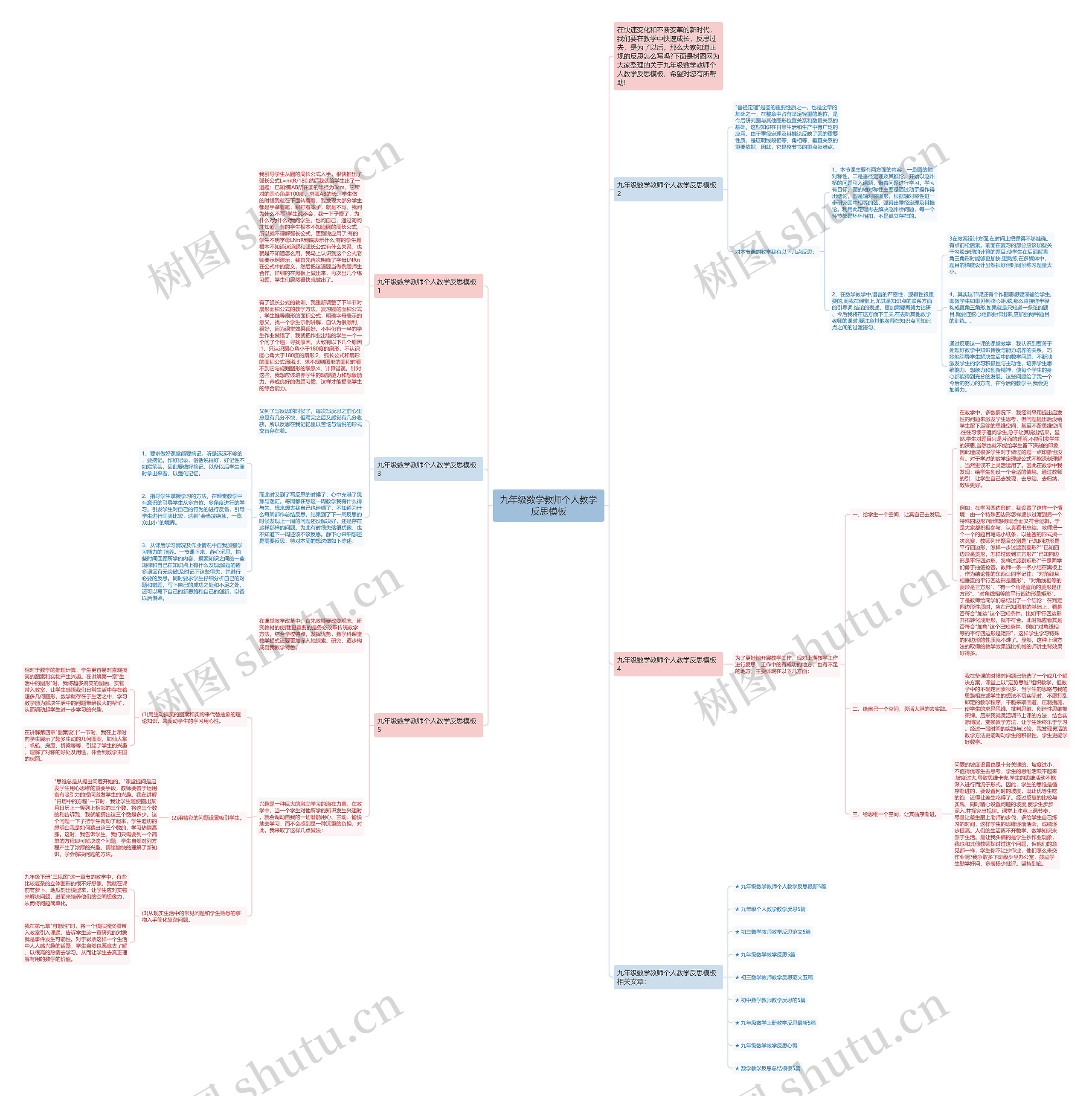
九年级数学教师个人教学反思思维导图包含到教学反思的模板，该模板包含了教学过程的调整和改进，和学生出错的问题分析和解决方法。通过对圆的弧长公式和扇形面积公式的教学反思，教师意识到需要加强学生的观察能力和想象能力，养成良好的做题习惯，以提高学生的综合能力，在关于“垂径定理”的教学中，教师通过问题引入和动手操作的方式带着学生学习，学习有目标，进一步研究圆中相等的弦和弧，得出了垂径定理推论。