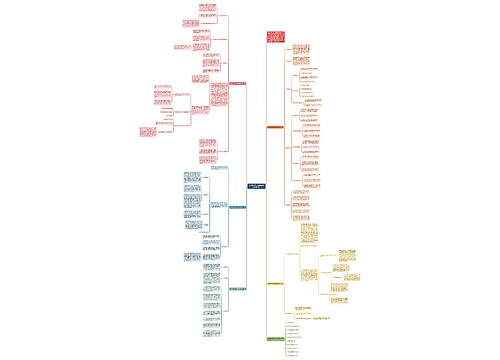
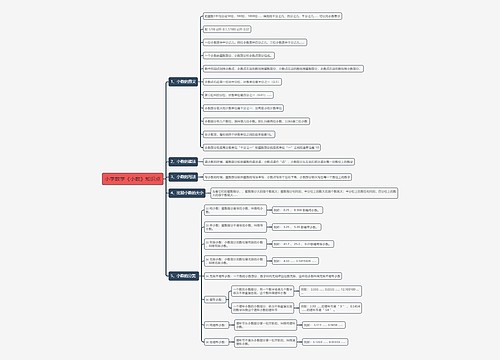
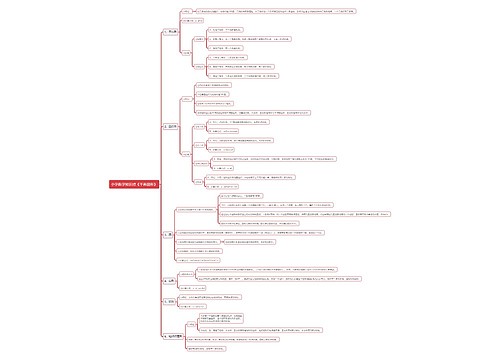
分式的运算人教版数学八年级上册教案思维导图
人生岁月几度寒
2023-04-04
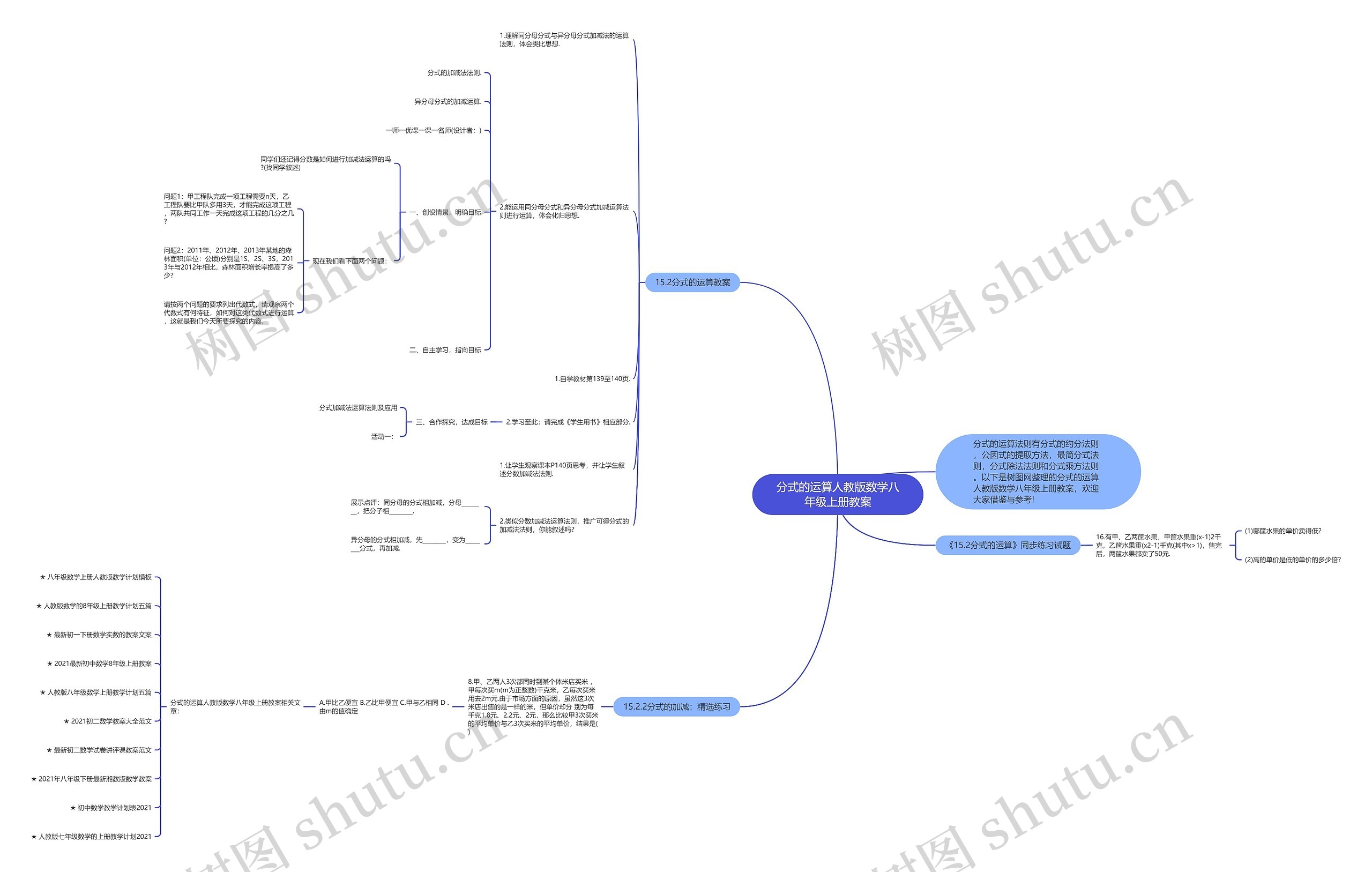
分式的运算法则,包含约分法则、公因式提取方法、最简分式法则、分式除法法则和分式乘法则,通过列举甲、乙工程队和某地森林面积,引导学生找出同分母分式和异分母分式的加减法法则,学生需要自学教材并完成相应练习,最后合作思考并达到目标,本模板还提供了相关试题及教学计划模板。
思维导图大纲
相关思维导图模版
乘法公式人教版数学八年级上册教案思维导图
 茶饭无心
茶饭无心树图思维导图提供《乘法公式人教版数学八年级上册教案》在线思维导图免费制作,点击“编辑”按钮,可对《乘法公式人教版数学八年级上册教案》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:5faf76e310ff3068593d59ce773260a4
二次根式的加减人教版数学八年级上册教案思维导图
 孤街浪徒
孤街浪徒树图思维导图提供《二次根式的加减人教版数学八年级上册教案》在线思维导图免费制作,点击“编辑”按钮,可对《二次根式的加减人教版数学八年级上册教案》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:2819ac7438d7d4d281db5d35fd31fd76