初一上册数学教案思维导图

定格苍凉

2023-04-04

浏览量: 7

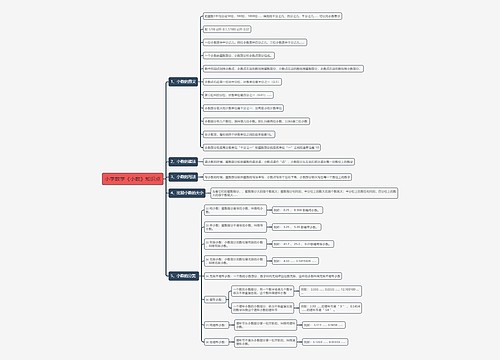
初一上册数学教案

初一

上册

数学

教案

初一上册数学教案思维导图相关的内容，数学课件的重要性，和初一上册数学教案的重点和难点都有所包含，教学目标和教学过程，包含有理数的概念和分类、集合，教学重点在于正确理解分类的标准和有理数的概念，需要引导学生思考、讨论和交流，帮助学生掌握分类的方法和意义，练习题，帮助学生巩固所学内容。

思维导图大纲

初一上册数学教案（篇1）

教学目标1，掌握有理数的概念，会对有理数按照一定的标准进行分类，培养分类能力；

2，了解分类的标准与分类结果的相关性，初步了解"集合"的含义；

3，体验分类是数学上的常用处理问题的方法。

教学难点正确理解分类的标准和按照一定的标准进行分类

知识重点正确理解有理数的概念

教学过程（师生活动）设计理念

探索新知在前两个学段，我们已经学习了很多不同类型的数，通过上两节课的学习，又知道了现在的数包括了负数，现在请同学们在草稿纸上任意写出3个数（同时请3个同学在黑板上写出）．

问题1：观察黑板上的9个数，并给它们进行分类．

学生思考讨论和交流分类的情况．

学生可能只给出很粗略的分类，如只分为"正数"和"负数"或"零"三类，此时，教师应给予引导和鼓励．

例如，

对于数5，可这样问：5和5.1有相同的类型吗？5可以表示5个人，而5.1可以表示人数吗？（不可以）所以它们是不同类型的数，数5是正数中整个的数，我们就称它为"正整数"，而5.1不是整个的数，称为"正分数，，．••…（由于小数可化为分数，以后把小数和分数都称为分数）

通过教师的引导、鼓励和不断完善，以及学生自己的概括，最后归纳出我们已经学过的5类不同的数，它们分别是"正整数，零，负整数，正分数，负分数，’．

按照书本的说法，得出"整数""分数"和"有理数"的概念．

看书了解有理数名称的由来．

"统称"是指"合起来总的名称"的意思．

试一试：按照以上的分类，你能作出一张有理数的分类表吗？你能说出以上有理数的分类是以什么为标准的吗？（是按照整数和分数来划分的）分类是数学中解决问题的常用手段，这个引入具有开放的特点，学生乐于参与

学生自己尝试分类时，可能会很粗略，教师给予引导和鼓励，划分数的类型要从文字所表示的意义上去引导，这样学生易于理解。

有理数的分类表要在黑板或媒体上展示，分类的标准要引导学生去体会

练一练1，任意写出三个有理数，并说出是什么类型的数，与同伴进行交流．

2，教科书第10页练习．

此练习中出现了集合的概念，可向学生作如下的说明．

把一些数放在一起，就组成了一个数的集合，简称"数集"，所有有理数组成的数集叫做有理数集．类似地，所有整数组成的数集叫做整数集，所有负数组成的数集叫做负数集……；

数集一般用圆圈或大括号表示，因为集合中的数是无限的，而本题中只填了所给的几个数，所以应该加上省略号．

思考：上面练习中的四个集合合并在一起就是全体有理数的集合吗？

也可以教师说出一些数，让学生进行判断。

集合的概念不必深入展开。

创新探究问题2：有理数可分为正数和负数两大类，对吗？为什么？

教学时，要让学生总结已经学过的数，鼓励学生概括，通过交流和讨论，教师作适当的指导，逐步得到如下的分类表。

有理数这个分类可视学生的程度确定是否有必要教学。

应使学生了解分类的标准不一样时，分类的结果也是不同的，所以分类的标准要明确，使分类后每一个参加分类的象属于其中的某一类而只能属于这一类，教学中教师可举出通俗易懂的例子作些说明，可以按年龄，也可以按性别、地域来分等

小结与作业

课堂小结到现在为止我们学过的数都是有理数（圆周率除外），有理数可以按不同的标准进行分类，标准不同，分类的结果也不同。

本课作业1，必做题：教科书第18页习题1.2第1题

2，教师自行准备

本课教育评注（课堂设计理念，实际教学效果及改进设想）

1，本课在引人了负数后对所学过的数按照一定的标准进行分类，提出了有理数的概

念．分类是数学中解决问题的常用手段，通过本节课的学习使学生了解分类的思想并进

行简单的分类是数学能力的体现，教师在教学中应引起足够的重视．关于分类标准与分

类结果的关系，分类标准的确定可向学生作适当的渗透，集合的概念比较抽象，学生真正接受需要很长的过程，本课不要过多展开。

2，本课具有开放性的特点，给学生提供了较大的思维空间，能促进学生积极主动地参加学习，亲自体验知识的形成过程，可避免直接进行分类所带来的枯燥性；同时还体现合作学习、交流、探究提高的特点，对学生分类能力的养成有很好的作用。

3，两种分类方法，应以第一种方法为主，第二种方法可视学生的情况进行。

初一上册数学教案（篇2）

教学目标1，掌握数轴的概念，理解数轴上的点和有理数的对应关系；

2，会正确地画出数轴，会用数轴上的点表示给定的有理数，会根据数轴上的点读出所表示的有理数；

3，感受在特定的条件下数与形是可以相互转化的，体验生活中的数学。

教学难点数轴的概念和用数轴上的点表示有理数

知识重点

教学过程（师生活动）设计理念

设置情境

引入课题教师通过实例、课件演示得到温度计读数．

问题1:温度计是我们日常生活中用来测量温度的重要工具，你会读温度计吗？请你尝试读出图中三个温度计所表示的温度？

（多媒体出示3幅图，三个温度分别为零上、零度和零下）

问题2：在一条东西向的马路上，有一个汽车站，汽车站东3m和7.5m处分别有一棵柳树和一棵杨树，汽车站西3m和4.8m处分别有一棵槐树和一根电线杆，试画图表示这一情境．

（小组讨论，交流合作，动手操作）创设问题情境，激发学生的学习热情，发现生活中的数学

点表示数的感性认识。

合作交流

探究新知教师：由上述两问题我们得到什么启发？你能用一条直线上的点表示有理数吗？

让学生在讨论的基础上动手操作，在操作的基础上归纳出：可以表示有理数的直线必须满足什么条件？

从而得出数轴的三要素：原点、正方向、单位长度体验数形结合思想；只描述数轴特征即可，不用特别强调数轴三要求。

从游戏中学数学做游戏：教师准备一根绳子，请8个同学走上来，把位置调整为等距离，规定第4个同学为原点，由西向东为正方向，每个同学都有一个整数编号，请大家记住，现在请第一排的同学依次发出口令，口令为数字时，该数对应的同学要回答"到"；口令为该同学的名字时，该同学要报出他对应的"数字"，如果规定第3个同学为原点，游戏还能进行吗？学生游戏体验，对数轴概念的理解

寻找规律

归纳结论问题3：

1，你能举出一些在现实生活中用直线表示数的实际例子吗？

2，如果给你一些数，你能相应地在数轴上找出它们的准确位置吗？如果给你数轴上的点，你能读出它所表示的数吗？

3，哪些数在原点的左边，哪些数在原点的右边，由此你会发现什么规律？

4，每个数到原点的距离是多少？由此你会发现了什么规律？

（小组讨论，交流归纳）

归纳出一般结论，教科书第12的归纳。这些问题是本节课要求学会的技能，教学中要以学生探究学习为主来完成，教师可结合教科书给学生适当指导。

巩固练习

教科书第12页练习

小结与作业

课堂小结请学生总结：

1，数轴的三个要素；

2，数轴的作以及数与点的转化方法。

本课作业1，必做题：教科书第18页习题1.2第2题

2，选做题：教师自行安排

本课教育评注（课堂设计理念，实际教学效果及改进设想）

1，数轴是数形转化、结合的重要媒介，情境设计的原型来源于生活实际，学生易于体验和接受，让学生通过观察、思考和自己动手操作、经历和体验数轴的形成过程，加深对数轴概念的理解，同时培养学生的抽象和概括能力，也体出了从感性认识，到理性认识，到抽象概括的认识规律。

2，教学过程突出了情竟到抽象到概括的主线，教学方法体了特殊到一般，数形结合的数学思想方法。

3，注意从学生的知识经验出发，充分发挥学生的主体意识，让学生主动参与学习活，并引导学生在课堂上感悟知识的生成，发展与变化，培养学生自主探索的学习方法。

初一上册数学教案（篇3）

教学目标1，掌握相反数的概念，进一步理解数轴上的点与数的对应关系；

2，通过归纳相反数在数轴上所表示的点的特征，培养归纳能力；

3，体验数形结合的思想。

教学难点归纳相反数在数轴上表示的点的特征

知识重点相反数的概念

教学过程（师生活动）设计理念

设置情境

引入课题问题1：请将下列4个数分成两类，并说出为什么要这样分类

4，－2，－5，＋2

允许学生有不同的分法，只要能说出道理，都要难予鼓励，但教师要做适当的引导，逐渐得出5和－5，＋2和－2分别归类是具有较特征的分法。

（引导学生观察与原点的距离）

思考结论：教科书第13页的思考

再换2个类似的数试一试。

归纳结论：教科书第13页的归纳。以开放的形式创设情境，以学生进行讨论，并培养分类的能力

培养学生的观察与归纳能力，渗透数形思想

深化主题提炼定义给出相反数的定义

问题2：你怎样理解相反数定义中的"只有符号不同"和"互为"一词的含义？零的相反数是什么？为什么？

学生思考讨论交流，教师归纳总结。

规律：一般地，数a的相反数可以表示为－a

思考：数轴上表示相反数的两个点和原点有什么关系？

练一练：教科书第14页第一个练习体验对称的图形的特点，为相反数在数轴上的特征做准备。

深化相反数的概念；"零的相反数是零"是相反数定义的一部分。

强化互为相反数的数在数轴上表示的点的几何意义

给出规律

解决问题问题3：－（＋5）和－（－5）分别表示什么意思？你能化简它们吗？

学生交流。

分别表示＋5和－5的相反数是－5和＋5

练一练：教科书第14页第二个练习利用相反数的概念得出求一个数的相反数的方法

小结与作业

课堂小结1，相反数的定义

2，互为相反数的数在数轴上表示的点的特征

3，怎样求一个数的相反数？怎样表示一个数的相反数？

本课作业1，必做题教科书第18页习题1.2第3题

2，选做题教师自行安排

本课教育评注（课堂设计理念，实际教学效果及改进设想）

1，相反数的概念使有理数的各个运算法则容易表述，也揭示了两个特殊数的特征．这两个特殊数在数量上具有相同的绝对值，它们的和为零，在数轴上表示时，离开原点的距离相等等性质均有广泛的应用．所以本教学设计围绕数量和几何意义展开，渗透数形结合的思想．

2，教学引人以开放式的问题人手，培养学生的分类和发散思维的能力；把数在数轴上表示出来并观察它们的特征，在复习数轴知识的同时，渗透了数形结合的数学方法，数与形的相互转化也能加深对相反数概念的理解；问题2能帮助学生准确把握相反数的概念；问题3实际上给出了求一个数的相反数的方法．

3，本教学设计体现了新课标的教学理念，学生在教师的引导下进行自主学习，自主探究，观察归纳，重视学生的思维过程，并给学生留有发挥的余地．

初一上册数学教案（篇4）

《余角和补角》第2课时教案

教学目标：

知识与能力

能正确运用角度表示方向，并能熟练运算和角有关的问题。

过程与方法

能通过实际操作，体会方位角在是实际生活中的应用，发展抽象思维。

情感、态度、价值观

能积极参与数学学习活动，培养学生对数学的好奇心和求知欲。

教学重点：方位角的表示方法。

教学难点：方位角的准确表示。

教学准备：预习书上有关内容

预习导学：

如图所示，请说出四条射线所表示的方位角？

教学过程;

一、创设情景，谈话导入

在现实生活中，有一种角经常用于航空、航海，测绘中领航员常用地图和罗盘进行这种角的测定，这就是方位角，方位角应用比较广泛，什么是方位角呢？

二、精讲点拔，质疑问难

方位角其实就是表示方向的角，这种角以正北，正南方向为基准描述物体的方向，如"北偏东30°"，"南偏西40°"等，方位角不能以正东，正西为基准，如不能说成"东偏北60°，西偏南50°"等，但有时如北偏东45°时，我们可以说成东北方向。

三、课堂活动，强化训练

例1如图：指出图中射线OA、OB所表示的方向。

（学生个别回答，学生点评）

例2若灯塔位于船的北偏东30°，那么船在灯塔的什么方位？

（小组讨论，个别回答，教师总结）

例3如图，货轮O在航行过程中发现灯塔A在它的南偏东60°的方向上，同时在它北偏东60°，南偏西10°，西北方向上又分别发现了客轮B，货轮C和海岛D，仿照表示灯塔方位的方法，画出表示客轮B、货轮C、海岛D方向的射线。

（教师分析，一学生上黑板，学生点评）

四、延伸拓展，巩固内化

例4某哨兵上午8时测得一艘船的位置在哨所的.南偏西30°，距哨所10km的地方，上午10时，测得该船在哨所的北偏东60°，距哨所8km的地方。

（1）请按比例尺1：200000画出图形。

（独立完成，一同学上黑板，学生点评）

（2）通过测量计算，确定船航行的方向和进度。

（小组讨论，得出结论，代表发言）

五、布置作业、当堂反馈

练习：请使用量角器、刻度尺画出下列点的位置。

（1）点A在点O的北偏东30°的方向上，离点O的距离为3cm。

（2）点B在点O的南偏西60°的方向上，离点O的距离为4cm。

（3）点C在点O的西北方向上，同时在点B的正北方向上。

作业：书P1407、9

初一上册数学教案（篇5）

《等式与方程》教案

教学目标

1、学生掌握方程的定义以及等式与方程的区别;

2、使学生掌握方程的解的定义，并且能某个值是否为指定方程的解。

教学重点

检验方程的解的方法

教学难点

区分等式与方程;等式与恒等式;恒等式与方程。

版面设计

方程与方程的解

一、等式与恒等式：

二、方程与整式方程：

三、方程的解与方程的根：

教学设计

一、复习引入：

⑴猜年龄：

将你的年龄乘以2再减去5，你的得数是多少?如果是21，我就能猜出你的年龄是13。

⑵找规律：

如果设小明的年龄为x岁，那么乘以2再减去5就是2x-5，所以得到方程(equation)：2x-5=21

二、新课传授：

1.等式与恒等式：

①等式：

像1+2=3，5.3-(-1.2)=6.5，x+2x=3x，x+3=5等这样用等号=来表示相等关系的式子，叫做等式。

等式左边的式子叫做等式的左边;

等式右边的式子叫做等式的右边;

等式的一般形式是：A=B

②恒等式：

像1+2=3，5.3-(-1.2)=6.5，x+2x=3x，a+b=b+a等这样等号两边的值永远相等的式子叫做恒等式。

2.方程与整式方程：

①方程：

这种含有未知数的等式叫做方程。

②整式方程：

方程的两边都是整式时，称为整式方程。

【练习】：课后1、2两题(指定学生口答)

1.方程的解与方程的根：

①方程的解：

能使方程左、右两边的值相等的未知数的值叫做方程的解;

②一元方程：

只含有一个未知数的方程称为一元方程;

一元方程的解也叫做方程的根。

2.一元一次方程：

只含有一个未知数，并且未知数的次数是1的整式方程叫做一元一次方程。

例检验下列各数是不是方程7x+1=10-2x的解：

⑴x=1;⑵x=-2。

解：⑴将x=1分别代入方程的左、右两边，得

左边=71+1=8，

右边=10-21=8，

∵左边=右边，

x=1是方程7x+1=10-2x的解。

⑵将x=-2分别代入方程的左、右两边，得

左边=7(-2)+1=-13，

右边=10-2(-2)=14，

∵左边右边，

x=-2不是方程7x+1=10-2x的解。

三、作业：

课后习题

同步练习

初一上册数学教案（篇6）

《整式的加减》教案

一、三维目标。

（一）知识与技能。

能运用运算律探究去括号法则，并且利用去括号法则将整式化简。

（二）过程与方法。

经历类比带有括号的有理数的运算，发现去括号时的符号变化的规律，归纳出去括号法则，培养学生观察、分析、归纳能力。

（三）情感态度与价值观。

培养学生主动探究、合作交流的意识，严谨治学的学习态度。

二、教学重、难点与关键。

1、重点：去括号法则，准确应用法则将整式化简。

2、难点：括号前面是—号去括号时，括号内各项变号容易产生错误。

3、关键：准确理解去括号法则。

三、教具准备。

投影仪。

四、教学过程，课堂引入。

利用合并同类项可以把一个多项式化简，在实际问题中，往往列出的式子含有括号，那么该怎样化简呢？

五、新授。

现在我们来看本章引言中的问题：

在格尔木到拉萨路段，如果列车通过冻土地段要t小时，那么它通过非冻土地段的时间为（t-0.5）小时，于是，冻土地段的路程为100t千米，非冻土地段的路程为120（t-0.5）千米，因此，这段铁路全长为100t+120（t-0.5）千米①冻土地段与非冻土地段相差100t—120（t-0.5）千米②上面的式子①、②都带有括号，它们应如何化简？

利用分配律，可以去括号，合并同类项，得：

100t+120（t-0.5）=100t+120t+120（-0.5）=220t-60

代数式苏教版数学初一上册教案思维导图